|
Глава I.
Лестница «на сколько»
Арифметическая прогрессия
Рассмотрим следующий ряд чисел:
40, 43, 46, 49, 52, 55, 58,...
Нетрудно заметить, что каждое число этого ряда получается из предыдущего путём прибавления одного и того же числа 3. Такой ряд чисел называется, как мы знаем, арифметической прогрессией. Числа, входящие в ряд, называются членами прогрессии; постоянная прибавка — «разностью» прогрессии.
Приведём ещё пример. Ряд чисел
25, 29, 33, 37, 41, 45, 49,
— есть арифметическая прогрессия, — здесь первый член равен 25; разность прогрессии равна 4.
Обычно члены прогрессии обозначаются буквами a1, a2, a3, ..., разность — буквой d.
В данном примере: a1= 25; a2 = 29; a3 = 33,...; d = 4; маленькая цифра справа внизу около буквы а указывает порядковый номер члена ряда.
В приведённых примерах каждое последующее число больше предыдущего; такая прогрессия называется возрастающей. Если же последующее число меньше предыдущего, то прогрессия называется убывающей. Например, ряд
50, 44, 38, 32, 26, 20, 14
есть убывающая арифметическая прогрессия. Здесь разность d — отрицательна, именно d = — 6.
Арифметическую прогрессию можно представить на чертеже (черт. 1).
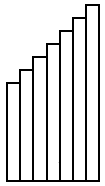
черт. 1
Здесь каждый член прогрессии представлен прямоугольником. Пусть ширина каждого прямоугольника равна 1 см; высоты прямоугольников равны последовательно 15 см, 19 см, 23 см, 27 см и т. д., площади этих прямоугольников будут равны соответственно 15 кв. см, 19 кв. см, 23 кв. см, 27 кв. см и т. д.
Арифметическую прогрессию можно назвать числовой лестницей «на сколько», так как каждый последующий член «на сколько-то единиц» больше предыдущего. В III главе настоящей книги будет рассмотрена прогрессия другого рода, лестница «во сколько». Изучение свойств этих двух прогрессий и их сопоставление поведёт нас к основной теме книги — к идее логарифма.
При рассмотрении арифметической прогрессии могут возникнуть следующие два основных вопроса:
1) Как по первым нескольким членам прогрессии определить любой её член, например, а30?
2) Как определить сумму некоторого числа последовательных членов прогрессии, например, сумму 30 членов?
Начнём с первого вопроса.
Пусть дана прогрессия 15, 19, 23, 27, 31,... Требуется определить сразу 30-й член этой прогрессии.
Обратимся к нашему черт. 1; надо найти высоту 30-го столбика. Эту высоту найдём, если к высоте первого (основного) столбика прибавим высоту подъёма, который даётся 29 ступеньками,.ведущими от 1-го к 30-му столбику.
Подъём одной ступеньки в нашем примере равен 4см; подъём, образуемый 29 ступеньками, равен d • 29 = 4 • 29 = 116 см.
Поэтому высота 30-го столбика равна: 15 + 4 • 29 = 15 + 116= 131 см.
Таким образом: а30 = а1 + 4 • 29 = а1 + d • 29 или же
а30 = а1 + d (30 —1).
Если бы требовалось найти 20-й член прогрессии, то мы написали бы:
а20 = а1 + d (20 —1).
Для члена прогрессии с нумером п получаем:
аn = а1 + d (n —1). (1)
Приведём пример применения этой формулы.
Завод сельскохозяйственных орудий выпустил в январе 800 машин. Затем он стал повышать свою продукцию каждый месяц на 25 машин. Сколько машин завод выпустил в декабре?
В данном случае а1 = 800; d = 25; n =12.
Согласно формуле, пишем:
а12 = а1 + d • 11; а12 = 800 + 25 • 11 = 800 + 275 = 1075.
***
Перейдём ко второму вопросу — нахождению суммы членов прогрессии.
Пусть дана прогрессия 25, 29, 33, 37, 41, 45, 49. Требуется найти сумму 7 членов этой прогрессии.
Для небольшого числа членов эту задачу можно было бы решить путём простого подсчёта. Но если бы требовалось найти сумму 700 членов, 7000 членов и т. д., то непосредственное сложение потребовало бы много времени. Желательно найти формулу, позволяющую решать такие задачи быстро и легко.
Чтобы получить эту формулу, обратимся к прежней модели.
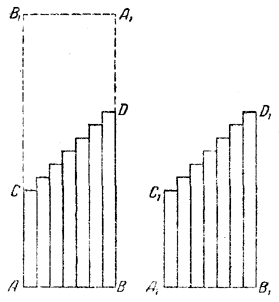
черт.2
На черт.2 построена ступенчатая фигура для прогрессии 25, 29,33, 37, 41, 45, 49. Ширина каждого столбика равна 1 см; длина равна соответственно 25 см, 29 см и т. д. Очевидно, сумма членов прогрессии численно равна площади фигуры ACDB в квадратных сантиметрах. Построим ещё одну фигуру A1C1D1B1, в точности равную фигуре ACDB. Приложим фигуру A1C1D1B1 к фигуре ACDB так, как показано
на чертеже пунктиром.
В результате получим прямоугольник АВА1В1 .
В этом прямоугольнике длина стороны АВ1 равна сумме AC + CB1 = AC + B1D1.
Ширина прямоугольника равна AB = 7 см.
Площадь прямоугольника АВ1А1В равна (АС + BD) • АВ; но
АС численно равно первому члену прогрессии а1 = 25,
BD — последнему её члену аn
= 49;
основание же АВ численно равно числу членов прогрессии n = 7.
Поэтому получаем:
Площадь прямоугольника равна (25+ 49) •7 кв. ед.
Но так как площадь АСDВ равна половине прямоугольника, то отсюда заключаем:
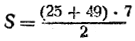
или в общем виде:
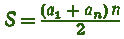 (2) (2)
Эта формула имеет весьма частые применения в различных отделах математики.
Простейшей арифметической прогрессией является ряд последовательных чисел
1, 2, 3, 4, 5, 6...,
называемый натуральным рядом. Для нахождения суммы этого ряда, взятого до некоторого числа п включительно, можно применить вышеуказанную формулу.
В этом случае а1 = 1, аn = n , а потому:
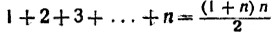 (3) (3)
Например,
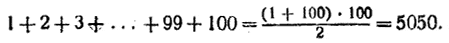
Мы дали вывод основной формулы (2) при помощи геометрической модели. Дадим теперь её вывод арифметическим путём.
Рассмотрим сначала сумму натуральных чисел от 1 до некоторого числа n —1, то есть сумму первых n —1 натуральных чисел; обозначим эту сумму буквой S:
S = l + 2 + 3 + ... + (n —3) + (n —2) + (n — 1).
Подпишем под нашим рядом тот же ряд, но в обратном порядке:
S = l + 2 + 3 + ... + (n —3) + (n —2) + (n — 1),
S = (n — 1) + (n — 2) + (n — 3) + ... + 3 + 2 + 1.
Ясно, что сумма двух членов, один из которых подписан под другим, равна числу п, т. е. сумме первого и последнего членов ряда. Число таких пар равно числу членов исходного ряда, т. е. п — 1. Следовательно, сумма этих двух совершенно одинаковых рядов 2S равна п(п— 1), а сумма одного исходного ряда равна:
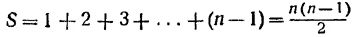
Просмотрев внимательно ход наших рассуждений, мы убедимся, что он повторяет слово в слово (правда, на другом языке — арифметическом) геометрический вывод, только что детально разобранный нами.
Те же рассуждения можно было бы повторить и для арифметического вывода формулы для суммы членов любой арифметической прогрессии с первым членом а1 , последним аn и разностью d. Но мы теперь достаточно подготовлены для того, чтобы понять и более формальный, но зато более короткий вывод. Обозначая сумму членов этой прогрессии
снова буквой S, будем иметь:
S = а1 + а2 + а3+...+ аn = а1 + (а1 + d) + ... + [а1+
( n — 1 )d ]
(каждый член мы заменили его выражением через первый член и разность). Раскроем теперь все скобки и приведём подобные члены:
S = nа1 + d [ l +2 + 3 +...+ (n — 1)].
Используя найденное нами выражение для суммы , l +2 + 3 +...+ (n — 1), получим
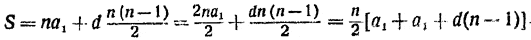
Но мы уже видели, что а1+ d ( n — 1 ) равно последнеиу члену прогрессии, т. е. аn. Следовательно, в конечном итоге получим:
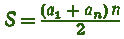
— ту же формулу, которую мы получили геометрическим путём.
Выведем ещё одну специальную формулу, которая будет нам полезна в дальнейшем.
Пусть требуется найти сумму ряда:
1+2 + 3 +... + 18 + 19 + 20 +19 + 18+...+3 + 2 + 1.
] Можно было бы вычислить её по общей формуле, взяв два раза сумму
1+2 + 3 +... + 18 + 19
и прибавив число 20. Но задачу можно решить короче, если заданный ряд чисел представить в виде двух строк:
1 2 3 4 5 ... 18 19
20
19 18 17 16 15 ... 2 1
Мы получим всего 20 столбцов; сумма чисел в каждом столбце равна 20 (последний столбец состоит из одного числа). Поэтому общая сумма равна 20•20 = 400. Это решение можно иллюстрировать чертежом (черт. 3).
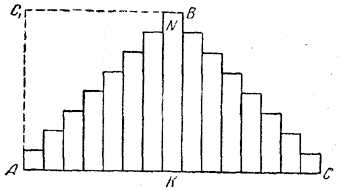
черт. 3
На чертеже дана ступенчатая фигура; взято п = 8.
Площадь фигуры ABC в кв. см равна:
1 +2 + 3 + 4 + 5 + 6 + 7 + 8 + 7 + 6 + 5 + 4 + 3 + 2 +1.
Eсли сделать разрез вдоль прямой NK, затем фигуру NKC повернуть и приложить зубцами к фигуре АВК, то получим квадрат АКВС1 со стороной, равной 8 см. Поэтому вышенаписанная сумма равна 82 = 64. Общая формула такова:
1+2 + 3 + ...+ ( n — 1 ) + n + ( n — 1 ) + ... + 3 + 2 + 1= n2 (4)
|