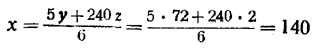|
Глава II. «На сколько» и «во сколько» Комбинирование отношений.
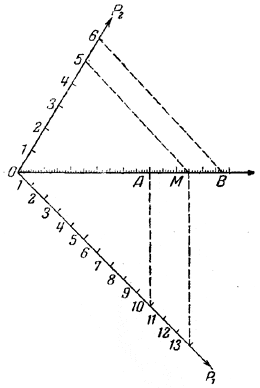
Читателю известно, как отношения применяются при решении задач. Однако эти применения становятся более широкими благодаря тому, что можно из двух, трёх, четырёх,... отношений образовать одно. Поясним это примером. Пример. Заводоуправление увеличило число станков в 2 раза: в то же время, благодаря принятым мерам рационализации, производительность труда повысилась на 25%. Требуется узнать во сколько раз увеличилась продукция завода. Здесь мы имеем одно увеличение в отношении (1 —>2) и другое в отношении (100 —> 125), или (4—>5). Задача состоит в том, чтобы узнать результат этих двух изменений. Решим задачу следующим образом. После увеличения числа станков вдвое завод будет выпускать вместо одной единицы продукции две такие единицы. Но повышение производительности труда таково, что вместо каждых 4 единиц выпускается 5. Поэтому надо указанные 2 единицы умножить на коэффициент 5/4 . Получим: 2 • 5/4 = 2,5 единицы. В результате вместо 1 единицы будет выпускаться 2,5 единицы. Коэффициенты изменения k1 = 2 и k2 = 1 1/4 как бы сливаются в один коэффициент k = 21/2, который, как легко заметить, получился в результате их перемножения. Допустим теперь, что после этих мероприятий на заводе образовалась группа стахановцев, которая указала новые приёмы работы, повышающие производительность труда ещё на 30%. Увеличение на 30% означает изменение в отношении (100—> 130), или же (10—> 13). Надо учесть эту величину нового отношения k3 = 13/10, а для этого надо прежнюю продукцию умножить на дробь 13/10. В результате получим: 2,5 • 13/10 = 3,25. Итак, окончательно, в результате всех мероприятий выпуск продукции достигает 325% первоначальной продукции. Коэффициент увеличения равен 13/4. Последний коэффициент k = 13/4 получился в результате слияния трёх коэффициентов: k1 = 2/1 ; k2 = 5/4; k3 = 13/10, т. е. в результате их перемножения. Ввиду того, что задачи, в которых несколько отношений сливаются в одно, часто встречаются в жизненной практике, остановимся, на таких задачах подробнее. Задача 1. Оборот кооператива поднялся за год на 30%; за второй год он поднялся на 20%. На сколько процентов поднялся оборот кооператива за два года? Решение. Примем первоначальный оборот за 100%, или 100 долей. Тогда, после первого повышения, которое выражается отношением (100 —> 130), или (10—>13), т. е. коэффициентом k1 = 13/10 оборот будет составлять 130 долей. К новому обороту надо применить второе увеличение в отношении (100 —> 120), или (5 —> 6). Такое изменение даётся коэффициентом k2 = 6/5. Перемножаем коэффициенты 130 • 6/5 = 156. Вместо 100 долей получается в результате 156, т. е. увеличение на 56%. Окончательный коэффициент k = 156/100 = 78/50 = 39/25 получился путём объединения коффициентов k1 = 13/10 и k2 = 6/5 . Вместо такого последовательного умножения можно сразу получить коэффициент увеличения оборота путём перемножения коэффициентов: 13/10 • 6/5 = 39/25 = 156/100 Присмотримся внимательнее к тому, что происходит с коэффициентами при их слиянии. При этом разборе воспользуемся черт. 15.
черт. 15 Исходная величина представлена отрезком ОА; обозначим длину ОА через а. Величина первого отношения k1 = 13/10 означает переход от отрезка ОА к отрезку ОМ. Такое изменение на чертеже достигается при помощи добавочной оси ОР1 с 10 и 13 делениями. К новому отрезку ОМ надо применить изменение в отношении (5 —> 6). С этой целью на чертеже берётся другая ось ОР2 с 5 и 6 делениями; вместо отрезка ОМ получаем отрезок ОВ. Если ОА равно 10 долям, то ОМ =13 таким долям. Так как число 13 не делится на 5, то придётся каждый из 13 отрезков, на которые разбит отрезок ОМ, разделить на 5 мелких долей. Тогда отрезок ОМ будет содержать 65 мелких долей, а отрезок ОА— 50 таких же долей. Если теперь отрезок ОМ разделить на 5 равных частей, то в каждой из них будет содержаться 65/5 = 13 мелких долей; но в таком случае отрезок ОВ содержит 13 • 6 = 78 мелких долей. В результате получается, что искомый отрезок ОА содержит 50 мелких долей, а отрезок ОВ — 78 таких же долей. Отношение OB/OA равно 78/50. Важно отметить, что число 50 получилось в результате того, что сперва отрезок ОА был разделён на 10 частей, а затем каждая часть ещё на 5 частей, т. е. ОМ в конце концов оказался разделённым на 50 частей. Число 50 есть произведение знаменателей обоих коэффициентов k1 = 13/10 и k2 = 6/5 . Число 78 получилось в результате того, что на оси ОР1 взяли 13 частей, а затем на оси ОР2 взяли 6 частей. Число 78 есть произведение числителей обоих коэффициентов k1 и k2. Итак, новый коэффициент k = 78/50 получается путём умножения обоих знаменателей и обоих числителей двух данных отношений, т. е. путём перемножения двух дробей. Отсюда вытекает: если к величине а надо применить последовательно два изменения с коэффициентами k1 и k2, то вместо них можно применить одно изменение с коэффициентом, k, который равен произведению первых двух: k = k1 • k2 Так мы получили указанное ранее правило. Задача 2. Допустим, что один кооператив получил распоряжение поднять цены на 10%, затем, вслед за ним, распоряжение понизить новые цены на 40%. Другой кооператив получил те же два распоряжения, но в обратном порядке: сперва понизить цены на 40%, затем повысить новые на 10%. Будут ли окончательные цены у обоих кооперативов одинаковы? Если нет, то у которого цена будет выше? Решение. После всего вышесказанного не трудно ответить на поставленный вопрос. В первом случае окончательный коэффициент изменения равен: k = k1 • k2 = 11/10 • 6/10 = 66/100 Во втором случае окончательный коэффициент равен: k = k1 • k2 = 6/10 • 11/10 = 66/100 Произведение в обоих случаях одно и то же (переместительный закон умножения). Окончательные цены в обоих кооперативах будут одни и те же. Задача 3. В саду устроена лотерея. Поставлены два сосуда с шарами. В одном сосуде имеется 4 красных и 16 белых, в другом — 6 красных и 14 белых шаров. Каждый играющий вынимает по одному шару из обоих сосудов. Играющий выигрывает, если оба вынутых шара окажутся красными. Каковы шансы на выигрыш? Примечание. Вынутые шары каждый раз возвращаются в те сосуды, из которых они были взяты, и перемешиваются. Первое решение. Вероятность вынуть красный шар из первого сосуда определяется отношением (4 : 20) = (1 : 5) или дробью р1 = 4/20 = 1/5 . Это означает, что если нынимать шары подряд, например, 100 раз, то из них примерно 20 раз появится красный шар. Чем больше число опытов, тем результат ближе к ожидаемому отношению. Допустим теперь, что в игре принимают участие 1000 человек. Если они все сначала вынимают шар из первого сосуда, то следует ожидать, что около 200 чел. вынут красный шар. Вынувшие белый шар из игры выбывают. Остающиеся 200 чел. будут продолжать игру: каждый из них имеет право вынуть шар из второго сосуда. Вероятность вынуть красный шар из второго сосуда определяется отношением (6 : 20) = (3 : 10), или же дробью р2 = 6/20 = 3/10 . Следовательно, можно рассчитывать, что из 200 чел., удачно получивших красный шар из первого сосуда, только 200 • 3/10= 60 чел. вынут красный шар также и из второго сосуда. Итак, из 1000 чел., участвующих в игре, лишь около 60 чел. окажутся выигравшими. Отношение числа выигравших к числу всех играющих есть (60 : 1000), или (6 :100), т. е. 6%. Таким образом из комбинирования отношении р1 = 4/20 и р2 = 6/20 получено новое отношение р = 6/100 . Этот результат вполне согласуется с вышеуказанным правилом сочетания двух коэффициентов: новое отношение равно произведению двух данных: р = р1 • р2 = 4/20 • 6/20 = 24/400 = 6/100 Заметим, что результат не изменится,если играющие сперва обратятся ко второму сосуду, а затем к первому. Второе решение. Перенумеруем все шары в первом сосуде, причём нумера 1—4 поставим на красных шарах, остальные нумера 5 —20 —на белых. Так же поступим с шарами во втором сосуде: нумера 1—6 поставим на красных, остальные на белых шарах. Если играющий вынимает по одному шару из обоих сосудов, то при этом может появиться любой нумер из первого сосуда в сочетании с любым нумером из второго сосуда,— нумер одного шара не зависит от нумера другого. Поэтому число всевозможных пар нумеров равно 20 • 20 = 400. На прилагаемой схеме показаны такие сочетания двух нумеров.
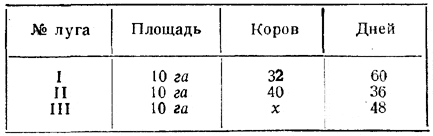
В каждой клетке первое число указывает нумер шара из первого сосуда, второе число — нумер шара из второго сосуда. Нет никаких оснований ожидать, что какая-либо пара должна появляться чаще других; поэтому мы считаем, что появление всех пар одинаково возможно. Какие же из этих пар нумеров дают выигрыш? Очевидно только те пары, в которых первое число не более 4, а второе — не более 6. На прилагаемой схеме они отделены жирной линией. Число этих пар равно 4 • 6 = 24. Итак, из 400 возможных пар только 24 пары нумеров дают право на выигрыш. Так как вероятность появления всех пар одинакова, то отсюда следует, что шансы на выигрыш определяются отношением (24:400) = (6 : 100), или дробью р = 24/400 = 6/100 . Вместе с тем имеет место равенство: р = 24/400 = 4/20 • 6/20 = р1 р2 . Это равенство ещё раз подтверждает вышеуказанное правило комбинирования отношений. На последнем примере с полной ясностью вырисовывается тот факт, что результат сочетаний двух отношений не зависит от того, в каком порядке эти отношения взяты. Ведь взять отношения в другом порядке—это значит, вынимать сначала шар из второго сосуда, а уж потом из первого. Такое изменение порядка на нашей схеме отразится лишь в замене строк столбцами и столбцов строками. Заметим ещё, что такой же ход решения будет иметь задача вычисления вероятностей в случае трёх, четырёх и более сосудов. Если обозначить вероятности вынуть красный шар из одного сосуда буквами р1 , р2 , р3 , р4 ,..... , то вероятность вынуть только красные шары из всех сосудов можно определить по формуле p = р1 • р2 • р3 • р4 ,..... В заключение рассмотрим две задачи, решения которых покажут, как в более сложных случаях используются понятия «на сколько» и «во сколько». Задача 4. (Задача Ньютона. Условие задачи имеет искусственный характер, так как трудно представить себе совершенно равномерный прирост травы ежедневно в течение месяца. Но мы всё же приводим задачу: она очень полезна как упражнение.) На одном лугу, площадью в 20 га, паслись 64 коровы и они за 60 дней съели траву, которая первоначально была на лугу, а также ту траву, которая выросла в течение этих 60 дней. На другом лугу в 30 га паслись 120 коров и они за 36 дней съели траву, имевшуюся первоначально, а также ту, которая выростала за эти дни. Сколько коров можно пустить на луг площадью в 40 га, чтобы они при тех же условиях могли прокормиться 48 дней? Решение. Прежде всего заметим, что, увеличивая площадь луга в несколько раз, можно и число пасущихся коров увеличить во столько же раз, потому что во столько же раз увеличится и первоначальный запас травы и количество травы, вновь вырастающей. Иными словами, число гектаров площади и число коров прямо пропорциональны. Поэтому видоизменим условия задачи таким образом, чтобы площадь луга во всех трёх случаях была одинаковой. В прилагаемой таблице показан результат этого изменения, причём площадь повсюду приводится к 10 га.
Если решить задачу в таком виде, т. е. найти значение х для площади в 10 га, то для получения окончательного ответа надо будет число х умножить на 4. Прежде чем перейти к решению задачи, обратим чнимание на то, из чего складываются количества корма на лугах. Во-первых, на всех трёх лугах (площадью по 10 га) имеется одинаковое первоначальное количество травы. Во-вторых, на лугах происходит равномерный рост травы, и это количество вновь вырастающей травы пропорционально числу дней. В результате общее количество корма на лугах не пропорционально числу дней; в этой непропорциональности и заключается трудность задачи. Переходим к решению. 1-й способ. Обозначим количество травы, имеющейся первоначально на лугу в 10 га, через А; количество травы вновь вырастающей за 1 день, через а. Тогда всё количество корма, которое получат коровы на первом лугу в 60 дней, равно А + 60а; всё количество корма на втором лугу, которое получат коровы в 36 дней, равно А + 36а. Если принять количество травы, которое съедает одна корова в 1 день, за одну порцию, то на первом лугу 32 коровы за 60 дней съедят 32 • 60 =1920 порций, а на втором лугу 40 коров за 36 дней съедят 40• 36=1440 порций. Итак, мы получаем уравнения: А + 60 а =1920 порций; А + 36 а = 1440 порций. Из сопоставления этих двух уравнений видно, что в первом случае количество травы на 24а больше, так как трава росла на 24 дня дольше. Именно поэтому в первом случае получилось на 1920—1440 = 480 порций больше. Отсюда следует, что 24а составляют 480 порций: 24а = 480; a = 480/24 = 20 (порций). Итак, за 1 день на лугу в 10 га вырастает трава в количестве 20 порций. Теперь можно определить и первоначальное количество травы. Если, например, взять I луг, то для него 60а = 60 • 20= 1200 порциям, откуда А = 1920 — 1200 = 720 порциям. После того как найдены величины А и а, легко закончить решение задачи. На третьем лугу коровы должны пастись 48 дней; поэтому можно рассчитывать на количество корма А + 48а или же 720 + 48 • 20 = 720 + 960 = 1680 порциям. Значит, имеется 1680 порций на 48 дней неизвестному количеству (х) коров; откуда: 48х =1680; х = 1680/48 = 35, т. е. на III луг (в 10 га) можно пустить 35 коров. При тех же условиях на лугу в 40 га, можно было бы прокормить 35 • 4 = 140 (коров). 2-й способ. Мы сейчас решили задачу, подсчитывая общее количество корма на лугу в порциях, путём сравнения «на сколько» этих количеств корма. Теперь решим нашу задачу, не определяя количества корма в порциях, путём сравнения «во сколько» запасов корма. Сравнивая условия на I и II лугах, мы видим, что количества коров, относятся между собой как 32 : 40 = 4 : 5; количества дней относятся как 60 : 36 = 5 : 3. Но количество съедаемого корма прямо пропорционально количеству коров и одновременно прямо пропорционально количеству дней. Следовательно, количества корма на I и на II лугу относятся между собой как произведения указанных коэффициентов 4/5 и 5/3 (слияние коэффициентов). k = k1 • k2 = 4/5 • 5/3 = 4/3 Пользуясь прежними обозначениями, мы запас корма на I лугу обозначим через A + 60a, на II лугу A+36a. Отсюда следует пропорция:
Эта пропорция означает, что если знаменатель дроби (слева) примем за 3 доли, то числитель будет содержать таких же 4 доли. Отсюда следует, что разность числителя и знаменателя составляет одну долю, т. е. I доля = 24а. Но тогда числитель равен 24а • 4 = 96а. Иными слонами, А + 60а = 96а; откуда А =36а. Итак мы не определили значений А и а (например, в порциях), но зато узнали соотношение величин A и a. Количество корма (считая подрастающий) на I лугу равно А + 60а = 36а + 60а = 96а. Количество корма на III лугу равно А + 48а (площадь его — та же, именно 10 га, а подрастает трава в течение 48 дней), т. е. 36а + 48а = 84а. Следовательно, на I лугу травы (вместе с подрастающей) в Но на III лугу х коров за 48 дней съедают 48х ежедневных порций травы, а на I лугу 32 коровы за 60 дней - 32 • 60 =1920 таких порций. Эти 1920 порций составляют 8/7 от 48х порций: 1920 = 8/7 • 48х. Отсюда Это — на лугу в 10 га. А на лугу в 40 га при тех же условиях можно прокормить вчетверо больше, т. е. 35 • 4 = 140 коров. Оба приведённых решения, несмотря на употребление букв, чисто арифметические. Они очень поучительны, дают хорошую гимнастику уму, а главное —показывают, как при решении сложных задач используются отношения «на сколько» и «во сколько». Но разумеется, проще и быстрее эту задачу можно решить с помощью алгебры. Приведём третье —алгебраическое — решение задачи Ньютона. Обозначим искомое количество коров на III лугу через х. Далее, через у обозначим первоначально находившееся на 1 га луга число ежедневно потребляемых-одной коровой порций травы; а через z обозначим количество тех же порций, ежедневно вырастающих на 1 га луга. Тогда первый луг даст нам 20у (столько было сначала), да ещё 20 • 60 • z (столько на 20 га подросло за 60 дней) порций травы. Но, с другой стороны, это количество порций должно равняться произведению числа коров на число дней пастьбы, т. е. должно дать 64 • 60 порций. Приравнивая друг другу эти количества, получим: 20у + 20 • 60z = 64 • 60. (I луг) Точно так же составим уравнения для двух других лугов: 30у + 30 • 36z = 120 • 36, (IIлуг) 40у + 40 • 48 z = 48 • х. (III луг) Понятное упрощение приведёт систему к такому виду: y + 60z = 192, y + 36z = 144, 5y + 240z = 6x. Первые два уравнения вовсе не содержат х и имеют одинаковые коэффициенты при у : они решаются в уме и дают 24z = 48, т. е. z = 2, а отсюда у = 72. Из третьего уравнения имеем:
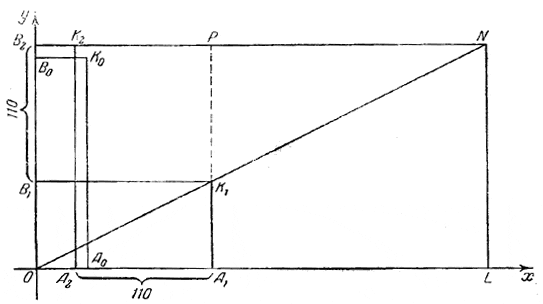
Получается, естественно, тот же ответ, что и при арифметическом решении, но значительно быстрее. Задача 5. (Индусская задача XII в.) А сказал своему другу В: «Дай мне 100 монет, и я буду в 2 раза богаче тебя». На это В ответил: «Дай мне 10 монет, и я буду в 6 раз богаче тебя». Сколько денег у каждого? В задаче мы имеем три положения (состояния): исходное фактическое положение (которое требуется определить); то положение, которое получилось бы при выполнении просьбы А; и то положение, которое получилось бы при выполнении просьбы В. Предположим, что выполнено желание А, т. е. что В передал А сто своих монет; при этом у А оказалось и 2 раза больше, чем у В. Примем это положение за исходное. Будем считать искомыми новые суммы А и В, т. е. решать новую задачу. Если мы эту новую задачу решим, то перейти к ответу на первоначально поставленную задачу будет нетрудно. Надо будет от А отнять 100 монет и прибавить их В. Теперь скажем: Если А отдаст В всего 100 +10=110 монет, то у А не только не будет больше в 2 раза, а наоборот —меньше в 6 раз чем у В. Итак, нам предстоит решить следующую видоизменённую задачу: Новая задача. А имеет в 2 раза больше чем В. Если от А отнять 110 монет и передать их В, то у В окажется в 6 раз больше чем у А. Сколько монет имеется у каждого? Дадим сначала арифметическое решение нашей задачи, очень изящное, но несколько длинное. Рассуждаем так. Сейчас А имеет в 2 раза больше монет чем В. Если В каким-либо путём получил 110 монет, то для сохранения отношения (2 : 1) следовало бы лицу А прибавить со стороны 220 монет (т. е. пропорционально количествам монет каждого). На самом же деле А не только не получает 220 монет, а наоборот, отдаёт 110 монет. Сопоставляя этот действительный случай с указанным предположением, имеем: вообр. В получает 110 монет; А получает 220 монет, При этом получаются такие соотношения: вообр. А имеет в 2 раза больше чем В. Примем новое количество монет у В (после получения 110 монет) за 1 долю. Тогда: вообр. В = 1 доля; А+ 220 это даёт А . . . 2 доли. Из этого сопоставления заключаем: в верхней строке А имеет на 220 +110 = 330 монет больше. Эти 330 монет составляют 2 — 1/6 = 15/6 = 11/6 доли. Итак: 11/6 доли = 330; откуда: 1 доля = 330 : 11/6 = 330 • 6/11 =180, т. е. новая сумма у В равна 180 монет. Отсюда находим прежнюю сумму у В, именно, 180 — 110 =70. Итак «новая» задача решена: В имеет 70 монет, А —140 монет. Переход к исходной задаче. Условие новой задачи получилось при предположении, что выполнено желание А, т. е. что А получил от В 100 монет. Для того чтобы вернуться к прежнему положению, надо отнять от А и передать В 100 монет. Получим: у А . . . 140 —100 = 40 монет, у В . . . 70 + 100 = 170 монет. Это и есть ответ на задачу. Иллюстрируем теперь решение задачи при помощи чертежа (черт. 16);
черт. 16 фактическое положение даётся прямоугольником ОА0К0В0. Здесь отрезок ОА0 изображает ту сумму денег, которую имел А, а отрезок ОВ0 — ту сумму денег, которую имел В. Если исполнить пожелание А, то создалось бы положение, даваемое прямоугольником ОА1K1В1 Именно это положение мы приняли за исходное во вспомогательной задаче. Если исходить от положения ОА1K1В1, то для выполнения пожелания В надо отложить: B1B2 = + 110 ед. вдоль оси Оу, А1А2 =—110 ед. на оси Ох (в направлении справа налево). Решение вспомогательной задачи можно проследить на графике следующим образом. ОА1 в 2 раза больше чем OB1 . Если отрезок ОВ1 получает прибавку В1В2 = 110 ед., то для сохранения величины угла K1ОА1 (т. е. отношения 2:1) следовало бы прибавить к ОА1 отрезок A1L, равный 220 ед., т. е. перейти к прямоугольнику OLNB2. Мы же, наоборот, отнимаем от ОА1 отрезок А1А2 = РК2 = 110 ед. Весь отрезок NК2 = NP + РК2 = 220 + 110 — 330 ед. Поэтому можно сопоставить два отношения: B2N : OB2= 2:1; В2К2 : ОВ2 = 1/6 : 1 . Если отрезок ОВ2 (т. е. сумму, которую будет иметь В при исполнении его пожелания) примем за 1 долю, то отрезок OL = B2N будет равен 2 долям, а отрезок В2К2 = 1/6 доли. Разность B2N— В2К2 = K2N равна 11/6 доли и в то же время K2N = 330 ед. Отсюда 1 доля, т. е. отрезок ОВ2=180 ед. и т. д. Эта задача быстрее решается алгебраически — путем составления следующей системы уравнений:
где х и у обозначают неизвестные суммы, бывшие первоначально у A и В. |