|
Глава II. «На сколько» и «во сколько» Случай равных отношений.
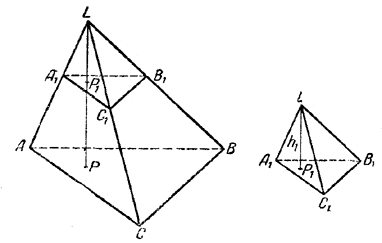
Мы видели, каким образом несколько заданных отношений соединяются в одно результирующее отношение. Обратимся теперь к рассмотрению того случая, когда заданные отношения все равны между собой, т. е. когда величины отношений совпадают. Иллюстрируем этот случай задачами. Задача 1. В парке устроена игра. Имеются 5 сосудов, в каждом из которых 60 красных и 40 белых шаров. Каждый играющий вынимает по одному шару из каждого сосуда. Выигрывает и получает премию тот, у кого все 5 вынутых шаров окажутся красными. Сколько премий должна приготовить администрация парка, если предполагается, что в игре примут участие 3000 человек. Решение. Вероятность вынуть красный шар из одного сосуда выражается отношением (60 : 100) или дробью р = 60/100 = 6/10 Как уже было установлено, в случае нескольких сосудов вероятность выигрыша р равна произведению вероятностей получить красный шар из каждого сосуда в отдельности. Но в данном случае все эти вероятности между собой равны, поэтому искомая вероятность р равна р = 6/10 • 6/10 • 6/10 • 6/10 • = ( 6/10 )5 Путём умножения получим: р = 7776/100 000. Эта дробь приблизительно равна 78/1000, или 7,8%. Полученный результат показывает, что из 1000 играющих в среднем будут выигрывать 78 человек. Если же в игре примут участие 3000 человек, то следует ожидать, что из них выиграют 78 • 3 = 234 человека. Так как в действительности могут произойти отклонения в ту или другую сторону, то администрация должна приготовить премии в несколько большем количестве. Вопрос о том, какие возможны отклонения от ожидаемого числа выигрышей и какова вероятность того или иного отклонения, составляет предмет особого раздела математики —теории вероятностей. Задача 2. Дана пирамида LABC (черт. 17). Высота её LP разделена в отношении 7 : 3, считая от вершины. Через точку деления P1 проведена плоскость, параллельная плоскости основания пирамиды. Она рассекает пирамиду на две части. Требуется сравнить объёмы обеих полученных частей.
черт. 17 Решение. Верхняя пирамида LA1B1C1 является как бы уменьшенной копией пирамиды LABC. Такие пирамиды называются подобными. Если высота LР1 содержит 7 долей, то вся высота LP содержит 7 + 3= 10 таких же долей, а потому отношение LP1: LP равно 7:10. Вследствие подобия тел, таково же будет отношение любых двух сходственных рёбер меньшей и большей пирамид. Величина же отношения объёмов двух подобных пирамид равна кубу (третьей степени) коэффициента подобия k. В нашей задаче взято значение k = 7/10. Поэтому отношение объёмов меньшей и большей пирамиды равно ( 7/10 )3 = 343/1000 Поэтому, если объём всей большой пирамиды принять за 1000 долей, то объём верхней части (при сечении) равен 343 долям, а объём нижней части равен 1000 — 343 = 657 долям. Как видим, нижняя часть пирамиды по объёму почти вдвое больше верхней части, хотя высота нижней (3 доли) значительно меньше высоты верхней (7 долей). |