Глава II.  

«На сколько» и «во сколько»

 Гипербола и одно из её важнейших свойств.

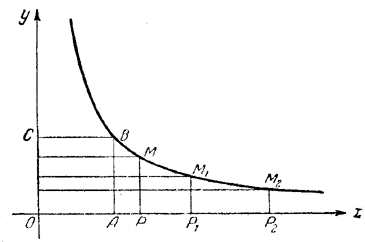
В предыдущей главе мы рассматривали лестницу «на сколько», в следующей главе мы будем изучать лестницу «во сколько».

Целью настоящей главы является выяснение взаимоотношения обоих понятий: на сколько и во сколько. Надо ясно видеть различие обоих понятий, но между ними имеется также внутренняя связь. И вот в математике оказалось возможным связать кратное и разностное отношения таким образом, чтобы они наглядно выступали рядом на одном и том же чертеже. При этом каждому отношению двух чисел  ставится в соответствие некоторое другое число k, и сочетанию двух «во сколько» k₁ • k₂ соответствует сочетание двух «на сколько» k₁ + k₂. Объяснению этого соответствия, т. е. перехода k —> k, будет посвящена 5-я глава книги под названием «Что такое логарифм». Здесь же мы дадим новой величине k наглядное, почти осязательное, представление в виде некоторой площади, ограниченной сверху кривой линией — гиперболой.

Прежде чем говорить о гиперболе, вспомним, что называют   прямой   и   обратной   пропорциональностью.

Две переменные называются пропорциональными, если при увеличении одной из них в несколько раз, во столько же раз увеличивается и другая величина. Так, пропорциональными являются радиус окружности и её длина; длина пути и работа по поднятию груза и т. д.

Иногда две переменные величины связаны так, что с увеличением одной из них в несколько раз —другая не возрастает, а уменьшается во столько же раз. Такие две величины называются обратно пропорциональными. Таковы, например, число рабочих и число дней, необходимых для кладки стены (чем больше рабочих кладут стену, тем скорее они закончат работу); таковы длина и ширина прямоугольника при заданной его площади (чем больше ширина прямоугольника, тем меньше должна быть его длина); таковы же, наконец, сопротивление проводника и сила электрического тока при постоянном напряжении (чем выше сопротивление проводника, тем меньше сила тока, проходящего через него). Построим график, показывающий связь двух величин, обратно пропорциональных друг другу. Возьмём две взаимно перпендикулярные прямые Ох и Оу (оси координат) (черт. 18).

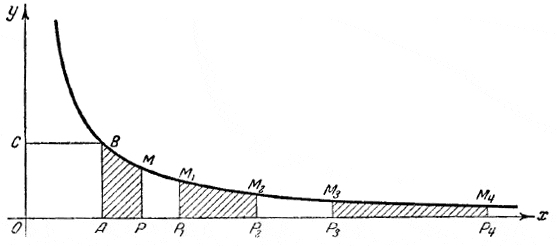
черт. 18

Будем строить прямоугольники, прилегающие к осям координат, так, чтобы площадь каждого из них была равна 1 кв. единице.   Если взять ОА=1 единице, то высоту АВ придётся взять равной также 1 единице, и мы получим квадрат ОАВС. Если OP₁ = 2 единицам, то высоту Р₁М₁ придётся взять равной ¹/₂ единицы; если ОР₂ = 3 единицам, то высоту P₂M₂ надо взять равной ¹/₃ единицы, и т. д.

Можно построить сколько угодно таких прямоугольников. В самом деле, для всякого отрезка ОР = х можно определить соответствующую высоту прямоугольника РМ, которую обозначим через у. Горизонтальный отрезок ОР называют обычно абсциссой точки М, а вертикальный отрезок РМ — ординатой точки М. Произведение абсциссы и ординаты ОР • РМ должно быть постоянно равным 1:

ху = 1,   откуда   у = ¹/_x .

Если нанести на чертёж весьма большое число произвольно взятых абсцисс и соответствующих им ординат и через концы ординат провести плавную линию, то получим кривую, которая называется «равнобочной гиперболой». Эта кривая даёт возможность наглядно представить себе, как изменяются две переменные, из которых одна обратно пропорциональна другой. Для этого вообразим, что точка Р движется по оси Ох вправо: тогда абсцисса ОР = х будет возрастать, точка М станет скользить по гиперболе, постепенно спускаясь по ней вниз, но никогда не достигая оси Ох, а ордината РМ будет уменьшаться, стремясь к нулю.

Если, наоборот, заставить х уменьшаться, стремясь к нулю, то точка Р будет приближаться к точке О, точка М будет подниматься по гиперболе влево, удаляясь от оси Ох; вместе с тем ордината у = РМ будет неограниченно возрастать.

Пусть теперь даны какие-нибудь два числа: x₁ = а, x₂ = b (пусть, например, x₁= 2, x₂= 3). Взяв отрезки OP₁ = x₁   и   ОР₂ = x₂, построим для них соответствующие ординаты Р₁М₁ = y₁ и Р₂М₂ = y₂. Такое построение можно сделать для любой пары чисел x₁, x₂.

Криволинейную площадь Р₁Р₂М₂М₁, т. е. плoщадь, ограниченную ординатами  Р₁М₁,    Р₂М₂, отрезком Р₁Р₂ и кривой линией М₁М₂ (дугой гиперболы — черт. 19),   мы сопоставим с отношением  .   

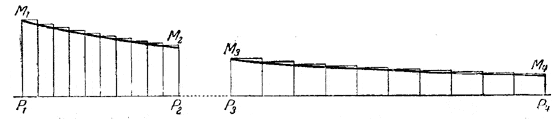
черт. 19

Связь  между   отношением  и   площадью  Р₁Р₂М₂М₁   очень   любопытна.

Оказывается, рассматриваемая площадь   обладает   важным свойством. Именно, как величина отношения  не изменяется, если оба числа x₁ и x₂ умнoжить   на  одно и то  же число т        ,   так  и площадь, построенная на интервале [x₁ ... x₂ ], равна площади, построенной  на  интервале [тx₁ ... тx₂ ].

Для простоты рассмотрим интервал от x₁ = 2 до x₂ = 3 и интервал от x₃ = 4 до x₄ = 6. Последние два числа в 2 раза больше первых двух. Отложим отрезки OP₁ = x₁, ОР₂ = x₂, ОР₃ = x₃, ОР₄ = x₄ (черт. 19). Построим на отрезках Р₁Р₂ и Р₃Р₄ криволинейные площади Р₁Р₂М₂М₁   и   Р₃Р₄М₄М₃. Докажем, что эти площади равны по величине, т. е. содержат одинаковое число квадратных единиц.

Так как эти площади ограничены кривой линией, то доказательство их равенства придётся вести косвенным путём. Представим себе, что интервал Р₁Р₂ разделён на 10 равных долей: так как Р₁Р₂ = l единице, то  длина одной доли равна 0,1 единицы. Построим ступенчатую фигуру, как показано на черт. 20 (на нём обе криволинейные трапеции изображены в большем масштабе, чем на черт. 19).

черт. 20

Каждый маленький прямоугольник имеет высотой левую ординату, и потому прямоугольники выходят зубцами за кривую линию. Точно такое же построение сделаем для второго отрезка Р₃Р₄. Длина Р₃Р₄ равна 2 единицам; длина одной доли будет равна ²/₁₀ = 0,2 единицы. Сравнивая любой из десяти прямоугольников второй фигуры с соответствующим прямоугольником первой фигуры (например, 4-й с 4-м, 5-й с 5-м и т. д.), видим, что у второй фигуры ширина прямоугольника в 2 раза больше, но одновременно высота каждого прямоугольника второй фигуры в 2 раза меньше, чем высота соответствующего прямоугольника первой фигуры, как это следует из способа построения гиперболы .

Итак, соответственные прямоугольники равны по площади. Отсюда следует, что и площадь всей второй ступенчатой фигуры равна площади всей первой ступенчатой фигуры.

Разделим теперь мысленно отрезки Р₁Р₂ и Р₃Р₄ каждый на 100 равных долей и построим опять ступенчатые фигуры, каждая из которых на этот раз состоит из 100 прямоугольников. Повторив прежние рассуждения, придём к выводу, что площади этих новых ступенчатых фигур также равны между собой.

Процесс такого одновременного подразделения обоих отрезков Р₁Р₂ и Р₃Р₄  можно  продолжать  как  угодно далеко, всё более увеличивая число долей, на которые делятся эти отрезки; каждый раз будем приходить к равенству площадей обеих ступенчатых фигур. Если брать число долей n =100, 200, 400, 800 и т. д., то левая ступенчатая фигура по величине площади подходит как угодно близко к криволинейной площади Р₁Р₂М₂М₁   и    одновременно правая — к криволинейной площади Р₃Р₄М₄М₃.

Разность между площадью ступенчатой фигуры и площадью соответствующей «гладкой» фигуры можно сделать меньше любого заданного числа, например, меньше чем 0,000001, меньше чем 0,000000001, и т. д.; для   этого   нужно   лишь   достаточно   мелко   разделить отрезки Р₁Р₂ и Р₃Р₄

Но площади обеих ступенчатых фигур в процессе их изменения всё время остаются равными между собой, а потому и площади обеих гладких фигур, к которым приближаются наши ступенчатые фигуры, не могут не быть равными между собой.

Мы взяли две криволинейные трапеции, опирающиеся на отрезки [2 ... 3] и [4 ... 6]. Если бы вторую из этих трапеций мы заменили трапецией, построенной на отрезке [6 ... 9],   то   прямоугольники    ступенчатой    фигуры, построенной для этой  трапеции,   были   бы   в три   раза шире и в три раза ниже, чем   прямоугольники   первой криволинейной фигуры, так   что  площадь  этой криволинейной трапеции была   бы такой   же,   как   и   у рассмотренных   ранее.   Ту   же   площадь,   очевидно,   будет иметь   всякая    криволинейная    трапеция,  построенная на отрезке [2т ... 3т].  Иначе   говоря,  если   изменять границы отрезка [а ... b], на котором построена криволинейная    трапеция,    оставляя    неизменным    отношение b : а, то площадь криволинейной трапеции не изменяется.

Во взятом примере отношение большего числа к меньшему равно 3:2. Поэтому обе рассмотренные нами криволинейные площади равны площади, опирающейся на отрезок [1 ... 1,5]; эта последняя является как бы мерой остальных. Но приведённое рассуждение сохраняет силу  для любого отношения х₂ : х₁.

Итак,   каждому   отношению двух   чисел    мы отнесли некоторую другую   величину —площадь  криволинейной   трапеции. Величина k не изменяется при одновременном изменении чисел х₁ и х₂ в одном и том же отношении, но при этом и площадь криволинейной трапеции остаётся неизменной. Плoщадь трапеции, опирающейся на интервал [х₁... х₂], как бы сопутствует величине отношения  . Но как измерить эту площадь? Приближённо    площадь    криволинейной    трапеции можно вычислить, если сделать весь чертёж  на миллиметровой бумаге в большом масштабе;  тогда можно подсчитать число квадратиков, заключённых внутри криволинейной площади. Но математика стремится к точности, и в VI главе этой книги читатель узнает формулу, дающую точную величину площади. Здесь же нам важно подчеркнуть, что именно отношение двух чисел  , и только оно, определяет величину площади, ограниченной дугой гиперболы у = ¹/_x , двумя ординатами и опирающейся на отрезок  [х₁... х₂].

Следствие. Из вышеизложенного можно извлечь следующее неожиданное и весьма важное следствие. Пусть произведение двух чисел х₁ • х₂ даёт третье число х₃.

Для конкретности будем считать, что х₁ = 2; х₂ = 3; х₃ = х₁ • х₂ = 2 • 3 = 6. На черт. 21 отложены соответствующие отрезки

ОР₁ = х₁,   ОР₂ = х₂,   OP₃ = х₃.

черт. 21

Площадь, ограниченную гиперболой и опирающуюся па отрезок [1 ...6], можно представить как сумму площадей, опирающихся на отрезок [1 ... 3] и на отрезок [3 ... 6]. Но отношение (6:3) равно отношению (2:1), а потому площадь, опирающуюся на отрезок [3 ... 6], можно заменить площадью, опирающейся на отрезок [1 ...2]. Отсюда следует: криволинейная   площадь, ограниченная гиперболой и расположенная на отрезке [1 ... 6], равна сумме площадей, ограниченных той же гиперболой и расположенных на отрезках [1 ... 2] и [1 ... 3]. Вообще, для всяких трёх чисел х₁ , х₂, х₃, удовлетворяющих условию х₃= х₁ • х₂ , площадь, ограниченная гиперболой и лежащая на отрезке [1 ... х₃], равна сумме площадей, ограниченных той же гиперболой и лежащих на отрезках [1 ... х₁] и [1 ... х₂]. Этот результат мы вкратце сформулируем так:

Теорема. Криволинейная площадь, ограниченная гиперболой и лежащая на интервале [1 ... х₁ х₂], равна сумме   площадей,   лежащих   на   интервалах [1 ... х₁] и [1 ... х₂]

В заключение покажем на нашей модели связь между пропорцией кратной (во сколько) и пропорцией разностной (на сколько).

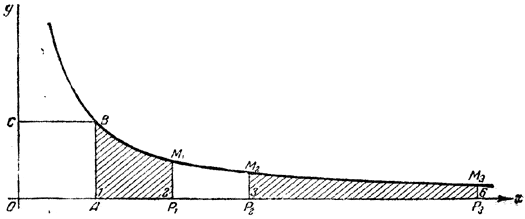
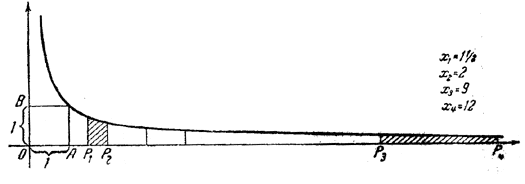
черт. 22

Пусть (черт. 22) имеется пропорция:

х₁ : х₂ =  х₃ : х₄ ;

например,

1¹/₂ :  2 =  9 :  12.

На чертеже четырём точкам с абсциссами, равными этим числам, соответствуют площади:

на  интервале     [1 ... х₁] = s₁;
»            »             [1 ... х₂] = s₂;
»            »             [1 ... х₃] = s₃;
»            »             [1 ... х₄] = s₄

(Точки с абсциссами х₁ , х₂ ,  х₃ , х₄отмечены буквами P₁, P₂, P₃, P₄) Но согласно изложенному, в силу указанной пропорции, т. е. равенства двух отношений, имеет место равенство площадей на интервалах [х₁ ... х₂]  и [х₃ ... х₄], т. е. равенство s₂ — s₁ = s₄ — s₃. Эти разности   на чертеже   представлены   двумя   заштрихованными площадками.

Итак, мы получили разностную пропорцию чисел s, сопровождающую кратную пропорцию чисел х.