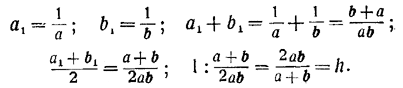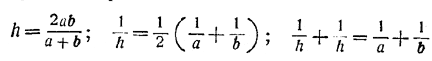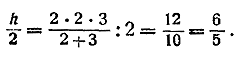Глава II.  

«На сколько» и «во сколько»

 Три средних.

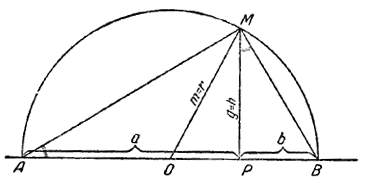
Мы знаем, что изменение линейных размеров какой-нибудь плоской (двумерной) фигуры, например, сторон треугольника, в некотором отношении (1—> k) сопровождается изменением её площади в отношении (1—> k²). Можно поставить обратную задачу: зная увеличение площади, например, в отношении (1 —>9), определить увеличение каждой стороны? Если в первой задаче мы некоторый переход или изменение (1—> k) повторяем два раза, то во второй задаче мы процесс перехода как бы «раскалываем» на две половины. Например, увеличение в отношении (1 —> 9) можно представить себе как бы составленным   из двух   равных  переходов: (1—>3) и (3—>9), так как второе отношение равно первому.

Приведём   ещё пример.   Пусть  требуется  увеличить добычу   угля  в шахте N  в 2 раза, причём дан срок в 2 года. Тогда через 1 год должно иметь место увеличение (1 —>q), через 2 года увеличение (q—>q²). Таким образом q² должно быть равно 2. Но если q²= 2, то q =√2 ≈  1,41. Следовательно, через 1 год увеличение должно составить 41%.

Рассмотрим теперь увеличение не от единицы, а от некоторой величины а до величины b, например, от 16 единиц до 80 единиц. И в этом случае можно поставить вопрос: какова та промежуточная величина (назовём её g), которая «раскалывает» интервал от а до b на два «равных» перехода (а —> g) и (g—>b), равноценных в вышеуказанном смысле. Можно поступить так. Переход а —> b, например, 16 —>80, равносилен некоторому определённому переходу 1—>k, в данном случае (1 —>5). Этот переход мы раскалываем «пополам»; получим (1 —> 2,24), потому что √5 ≈  2,24. Прилагаем «половину перехода» к исходной величине а; получим аk = 2,24а. При этом в результате получится переход

а—>2,24а

2,24а—> 5а = b.

Вставленная промежуточная величина получила название «среднего геометрического» двух данных чисел. Мы  получили её, приводя переход (а—>b) к переходу (1—>k), где     k = ^b/_a.

Можно определить среднее геометрическое другим путём. Так как для него имеем переход (а—> х —> b), где отношения ^x/_a и ^b/_x равны, то можно задачу нахождения х решить с помощью пропорции: а : х =  х : b, откуда x² = ab; х = √ab.

Это среднее х принято обозначать через g , от слова geometrica, что значит «геометрическая», так как оно встречалось ещё в древности при решении геометрических задач (именно задач на подобие фигур). Итак,

а : g =  g : b.

Рассмотрим пример геометрической иллюстрации величины g. Пусть (черт. 23) вдоль прямой линии от точки Р отложены отрезки РА длины а и РВ длины b. Из середины О всего отрезка АВ опишем полуокружность и в точке P восстановим перпендикуляр РМ. Тогда длина РМ  и  будет  средним  геометрическим g обоих чисел а и b.

черт. 23

Как читателю известно из курса геометрии, имеет место пропорция: АР : РМ = РМ : РВ; или a : h = h : b. А потому высота h является средним геометрическим величин а и b.

Чтобы яснее представить себе связь между средним геометрическим и средним арифметическим, докажем следующую теорему:

Теорема. Среднее геометрическое двух положительных чисел меньше их среднего арифметического *).

*) Если мы возьмём два одинаковых числа a и b = а, то их среднее  арифметическое будет  равно среднему геометрическому:

Чтобы учесть и эту возможность в формулировке указанной теоремы, слово «меньше» заменяют словами «не больше».

Ввиду важности этой теоремы, докажем её тремя способами.

1-й способ. На приведённом сейчас чертеже среднее геометрическое было представлено в виде высоты РМ = h. Так как сумма обоих чисел а + b равна длине диаметра АВ, то полусумма их т равна длине радиуса.

Имеем: т = ОA = ОВ = OM.

Тогда в прямоугольном треугольнике ОРМ катет РМ равен g, гипотенуза ОМ равна т. Но катет меньше гипотенузы, откуда g < m , что и требуется доказать.

2-й способ. Если числа a и b не равны друг другу, то  их разность   a — b  не  равна   нулю,   следовательно, квадрат  этой разности есть число положительное, т. е. большее чем нуль:

(a — b)² > 0.

Раскрывая скобки, получим:

a² — 2ab + b² > 0.

Прибавим к обеим частям этого неравенства по 4ab; это даст новое неравенство:

a² + 2ab + b² > 4ab   или   (a + b)² > 4ab,

что можно иначе записать так:

(a + b)² > (2√ab)².

Но если квадрат одного положительного числа больше чем квадрат другого, то и само первое число больше второго. Следовательно,

,

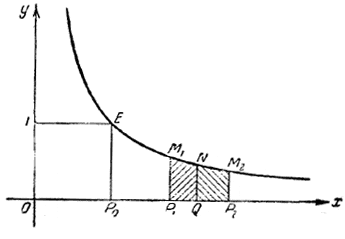
что и требуется доказать.

3-й способ. На черт. 24 на оси Ох отложены отрезки ОР₁ = а, ОР₂ = b.

черт. 24

Пусть среднее геометрическое этих чисел g изобразится отрезком OQ.

Согласно вышедоказаиному свойству гиперболы, если имеет место пропорция
OP₁: OQ = OQ : OP₂, то криволинейные площади M₁P₁QN и NQP₂M₂ должны быть равны, т. е. ордината QN должна делить площадь М₁Р₁Р₂М₂ пополам. Но если бы точка Q лежала ровно посредине между точками Р₁ и Р₂, то левая часть площади была бы больше правой, так как гипербола понижается слева направо.

Для того чтобы площадь разделилась пополам, необходимо, чтобы ордината QN была расположена левее середины отрезка Р₁Р₂. Таким образом, P₁Q должно быть меньше, чем QР₂, т. е. g — а < b — g, что и требуется доказать.

Помимо среднего геометрического и среднего арифметического в математике рассматривают ещё одно «среднее», носящее название среднего гармонического. Словесное определение его довольно громоздко; вот оно: «среднее гармоническое двух данных чисел есть число, обратное среднему арифметическому чисел, в свою очередь обратных заданным числам». Легче понять на конкретном примере, как образуется это «среднее»:

Принято  обозначать это  новое  «среднее»   буквой h (от французского слова harmonique — гармонический). Сосчитаем это h для взятых нами чисел 20 и 30:

Нетрудно также написать общую формулу для среднего гармонического. Имеем:

Таким образом среднее   гармоническое  определяется формулой:

Нетрудно видеть, что среднее гармоническое  можно определять и таким равенством:

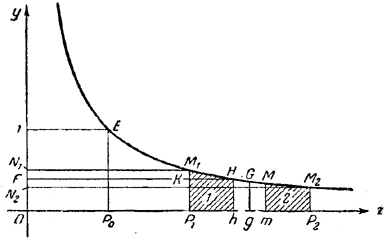
Покажем теперь, как можно построить среднее гармоническое, если  пользоваться   геометрической   моделью отношений.

черт. 25

На черт. 25 представлена гипербола, для каждой точки которой произведение
ОР•РМ = х • у= 1 . Пусть  длина  ОР₁ = а, ОР₂ = b.  Тогда   длина   ординаты P₁M₁ равна   ¹/_a= а₁;  ордината     Р₂М₂ = ¹/_b = b₁ .

При помощи горизонтальных прямых M₁N₁ и М₂N₂ отложим эти новые отрезки на оси Оу. Для этих обратных величин а₁  и b₁  берём   среднее  арифметическое,  т. е. точку F, лежащую посредине между точками N₁ и N₂. Из точки F проводим горизонтальную прямую до встречи с гиперболой в некоторой точке H; из точки Н проводим ординату Hh. Тогда длина отрезка Oh представит собой среднее гармоническое величин а и b.

Сравним теперь все три рассмотренные нами «средние» двух чисел а и b:

1)  среднее геометрическое

g = √a • b;    a : g =  g : b;    g • g = a • b;

2)   среднее арифметическое

3)  среднее гармоническое

Мы предполагаем, что а < b и что оба числа больше 1. Оказывается, что для любых двух неравных положительных чисел средние g,  m,  h  всегда располагаются в определённом порядке.

Выше мы уже показали, что среднее геометрическое g ближе к меньшему числу а. А это означает, что g меньше среднего арифметического m.  Итак

а < g < т < b.

Остаётся установить положение среднего гармонического. Можно показать, что среднее гармоническое h всегда меньше среднего геометрического g. Для этого достаточно показать, что на черт. 25 ордината hH делит площадь Р₁Р₂М₂М₁ так, что левая часть меньше правой (ранее было показано, что ордината gG делит эту же площадь пополам).

По построению гиперболы имеем: пл. OP₁M₁N₁ =   пл. OhHF = 1 кв. ед.

Отсюда следует, что площади прямоугольников FKM₁N₁ и P₁hHK равны.

Прибавляя к тому и другому прямоугольнику «криволинейный» треугольник KНM₁, получим: криволинейная площадь    FHM₁N₁ равна криволинейной площади P₁hHM₁. Таким же образом можно показать, что криволинейная площадь N₂M₂HF равна криволинейной площади hP₂M₂H.

Из    сравнения    криволинейных    узких    площадей FHM₁N₁  и N₂M₂HF следует, что первая площадь меньше второй.

Отсюда следует, что и площадь P₁hHM₁ меньше площади hP₂M₂H.

Итак, доказано,  что h < g. Таким обра-шм установлено расположение всех трёх «средних»:

a < h < g < m < b.

На черт. 25 отложены пять отрезков, соответствующих этим числам, на оси Ох:

OP₁ = a;    Oh = h;   Og = g;    Om = m;   ОР₂ = b.

Приведём в заключение любопытную теорему, связывающую все три «средних».

Теорема. Из трёх средних h, g, m  число g есть среднее геометрическое двух других.

Доказательство проще всего провести алгебраическим путём. Мы уже видели, что   Среднее геометрическое чисел т и h равно квадратному корню из их произведения, т. е. √mh. Вычислим этот корень:

А это как раз и нужно было доказать.

С гармоническим средним часто приходится иметь дело школьникам, хотя они и не называют его по имени. Рассмотрим, например, следующую известную всем задачу, по образцу которой решаются многие другие.

Задача. В бассейн ведут две трубы. Первая труба, действуя одна, наполняет его в 2 часа, вторая —в 3 часа. В какое время наполнится бассейн, если обе трубы будут действовать одновременно?

Посмотрим, какую часть бассейна наполняет одна 1-я труба, действуя в течение часа. Раз весь бассейн она наполняет за 2 часа, значит, за 1 час она наполнит его половину, т. е. ¹/₂. Точно так же 2-я труба, действуя одна в течение часа, наполнит ¹/₃ бассейна. Обе  трубы, действуя вместе, наполнят   в  течение   часа   ¹/₂ + ¹/₃ = ⁵/₆ бассейна.

Далее рассуждаем так: если ⁵/₆ бассейна наполняются за 1 час, то ¹/₆ наполнится за ¹/₅ часа, а весь бассейн — т. е. ⁶/₆  —  за ¹/₅ • 6 = ⁶/₅ часа (т. е. за 1 час 12 минут).

Приглядевшись внимательнее к выполненным действиям, мы заметим, что, в сущности, мы нашли половину среднего гармонического данных в условиях задачи чисел, т. е. чисел 2 и 3. Действительно:

Читатели без труда докажут самостоятельно следующую физическую теорему:

электросопротивление системы, состоящей из двух параллельно соединённых проводников, равно половине среднего гармонического собственных сопротивлений данных проводников.