|
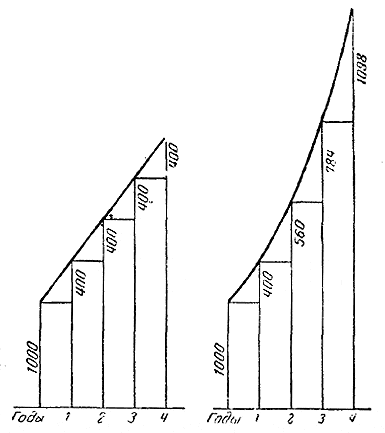
ГЛАВА III. ЛЕСТНИЦА «ВО СКОЛЬКО». Геометрическая прогрессия. Во второй главе книги мы подробно разобрали два способа сравнения величин: «на сколько больше» и «во сколько раз больше». Первый способ связан с вычитанием, второй — с делением. В первой главе мы рассматривали арифметическую прогрессию, или «лестницу на сколько», т. е. ряд величин, из которых каждая на одно и то же число больше предыдущей. В настоящей главе мы разберём прогрессию другого рода, а именно—лестницу «во сколько». Лестница «во сколько», или геометрическая прогрессия, это —такой ряд чисел, в котором каждое число получается путём умножения предыдущего на постоянный коэффициент к (знаменатель прогрессии). Примером геометрической прогрессии может служить ряд чисел: 5,10,20,... Здесь k = 2. Числа, образующие прогрессию, называются её членами. Арифметическая прогрессия была известна в самые отдалённые эпохи; о геометрической прогрессии мы находим первые отрывочные замечания в греческой математике лишь немногим более 2000 лет тому назад. Понять различие между геометрической и арифметической прогрессией можно из следующего примера: Директоры двух заводов А и В встретились на совещании. Из их беседы выяснилось, что оба завода выпустили за последний год одинаковые количества продукции, а именно по 1000 т металлических изделий. На совещании было решено добиваться дальнейшего роста продукции, причём был намечен ежегодный прирост на 40%. Директор завода А выполнял задание следующим образом. В первый год после совещания его завод выпустил на 40% больше, чем раньше, т. е. на две пятых, а именно: 1000 +1000 • 2/5 = 1000 + 400 =1400. За второй год завод выпустил ещё на 400 т больше, т. е. 1400 + 400=1800, и так далее. В результате выпуск изделий за последующие 4 года оказался таким: до совещания.......1000, Директор завода В поступил иначе. За первый год после совещания он выпустил на 40% больше, чем раньше, т. е. 1000 +1000 • 2/5 =1400 т. За второй год директор завода В добился дальнейшего, роста производительности труда, и завод выпустил за второй год на 40% больше, чем за первый год: 1400 + 1400 • 2/5 = 1400 + 560 = 1960 т. На третий год он составил план по тому же принципу: опять увеличить выработку на 40% по сравнению с предыдущим годом: 1960+ 1960 • 2/5 = 1960 + 784 = 2744 т. За четвёртый год завод В дал такую выработку: 2744 + 2744 • 2/5 = 2744 + 1098 = 3842. В результате выпуск изделий заводом В оказался следующим: до совещания.......1000, Заметим, что коэффициент увеличения здесь равен 7/5 , так как выпуск каждого года составляет 140% предыдущего года, 140%= 140/100 = 7/5 . Через 4 года директоры заводов А и В снова встретились на совещании и сравнили выработку обоих заводов. Оказалось, что завод В выпустил значительно больше изделий, чем завод A. Завод А сохранял всё время одну и ту же надбавку, равную 400 т в год. Завод В сохранял неизменным отношение выработки двух соседних лет, т. е. коэффициент увеличения k = 7/5 . Представим на графике продукцию того и другого завода (черт. 26).
Черт. 26 Приведём ещё один пример. Задача. Некто положил в банк 200 руб. В течение 5 лет он не получал денег. Банк в конце каждого года присчитывал 6% к его вкладу. Сколько получит вкладчик через 5 лет? Решение. Через 1 год вкладчик мог получить: 200 + 200 • 6/100 = 200 ( l + 6/100) = 200 • 1,06 = 212 руб. Через 2 года он мог получить: 212 + 212 • 6/100 = 212 ( l + 6/100) = 224,7 руб. Эту сумму можно записать в виде: (200 • 1,06) • 1,06 = 200 • 1,06 • 1,06 = 200 • (1,06)2 Через 3 года вкладчик мог получить: 224,7 (1 + 6/100) = 224,7 • 1,06 = 238,2 руб.; иначе эту сумму можно обозначить так: [200 (1,06)2] • 1,06 = 200 • (1,05)2 • 1,06 = 200 • (1,06)3 Через 4 года вкладчик мог получить: 238,2 • 1,06 = 252,5 руб. Эту сумму запишем ещё так: [200 • (1,06)3] • 1,06 = 200 • (1,06)3 • 1,06 = 200 • (1,06)4. Через 5 лет вкладчик получит: 252,5 • 1,06 = 267,6 руб. Эту сумму запишем так: [200 • (1,06)4] • 1,06 = 200 • (1,06)5. Проделаем то же самое в буквенных обозначениях. Если начальный вклад обозначим через а0, а коэффициент ежегодного увеличения вклада через k, то суммы, которые вкладчик может получить в конце первого, второго, третьего и следующих годов, можно записать следующими формулами: через 1 год: а1 = а0 • k, а1 = а0k; через 2 года: а2 = а1 • k, а2 = а0k2; через 3 года: а3 = а2 • k, а3 = а0k3; через 10 лет а10 = а9 • k, а10 = а0k10; ........................................................................ через n лет аn = аn-1 • k, аn = а0kn. Равенства первого столбца выражают именно то, что числа представляют собой геометрическую прогрессию, так как величина вклада в конце каждого года равна величине вклада предыдущего года, умноженной на один и тот же коэффициент k. Равенства второго столбца дают формулу для любого члена прогрессии. Коэффициент k, дающий отношение каждого члена прогрессии к предыдущему, принято обозначать буквой q; его называют «знаменателем» прогрессии. Формула для любого члена прогрессии запишется так: аn = а0 • qn *). (1) ------------------------------------------------------------------------------- *) Заметим тут же, что в учебниках принято эту формулу записывать иначе. У нас первый член прогрессии был обозначен а0 , второй а1, третий а2, и т. д В учебниках первый член прогрессии обозначают через а1, второй — через а2, третий — через а3 и т. д., и формула (1) записывается в таком виде: аn = а1 • qn-1 , причём аn сответствует нашему аn-1 , а а1 — нашему а0. --------------------------------------------------------------------------- Вычисление аn по формуле (1) гораздо сложнее, чем вычисление аn в случае арифметической прогрессии. Пусть, например, а0 = 20, q = 1,08 и требуется найти а30. Тогда по формуле (1) напишем: а30 = а0 • q30. Но как сосчитать (1,08)30? Перемножать 30 раз 1,08 весьма утомительно. Если требуется точный результат, то придётся иметь дело с огромным числом десятичных знаков. Очевидно, в таких случаях округляют получающиеся числа; надо, однако, следить за тем, чтобы эти округления в общем итоге не дали большого отклонения от искомого результата. В настоящее время такие вычисления делают весьма быстро и со значительной степенью точности при помощи таблиц логарифмов, но об этом речь будет дальше. Покажем теперь, как можно строить геометрическую прогрессию графическим путём. Пусть даны первый член и знаменатель прогрессии, например, а0 = 20; q =1,2.
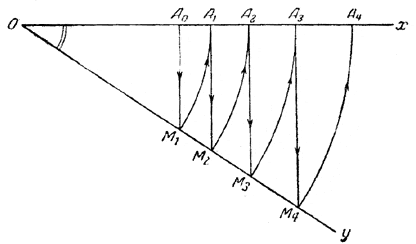
Черт. 27 Откладываем (черт. 27) вдоль горизонтальной оси Ох отрезок ОА0 = а0. Способом, указанным во второй главе (черт. 12), увеличиваем отрезок ОА0 , в отношении (1 —> q ), например, в отношении (1 —> 1,2), и отрезок ОА1, равный а0 • q , откладываем вдоль той же оси Ох (в нашем примере а0q = 20 • 1,2 = 24). Из точки А0 восставляем перпендикуляр к оси Ох; затем из точки О, как из центра, описываем радиусом, равным ОА1, дугу окружности до встречи с перпендикуляром в некоторой точке М1. Через точки О и М1 проводим прямую OY. Для построения дальнейших отрезков, дающих значения членов геометрической прогрессии, из точки А1 восставляем перпендикуляр до пересечения с прямой OY, где-нибудь в точке М2; затем из точки О, как из центра, описываем радиусом, равным ОМ2, дугу окружности до встречи с осью Ох в точке А2. Отрезок ОА2 представляет собой следующий член прогрессии а0q2. Если такого рода переходы совершать дальше A2—>М3—>A3; A3—>М4—>A4 и т. д., то на оси Ох отложатся отрезки ОА2, ОА3,ОА4, ОА5, ..., представляющие последовательные члены геометрической прогрессии аq2, аq3, аq4 и т. д. Чтобы показать правильность этого построения, надо рассмотреть пары соседних треугольников ОА0М1 и ОА1М2. Из их подобия следует:
Согласно построению, мы имеем ОА1 = OM1 = а0 • q; ОА0 = а0 , поэтому
Отсюда следует:
Кривая М2А2 есть дуга окружности; поэтому ОА2 также равно а0q2. Далее берём треугольники ОА1М2 и ОА2М3. Из их подобия следует:
или
откуда ОМ3 = а0q2 • q = а0q3 Отрезок ОА3 также равен аq3, и так далее. В тех случаях, когда не требуется большой точности, можно пользоваться этим графическим построением. Если сопоставить определения арифметической и геометрической прогрессий, то можно заметить следующую аналогию между ними. В арифметической прогрессии мы прибавляем одно и то же число для получения следующего члена, в геометрической прогрессии—умножаем для этого на один и тот же коэффициент. В арифметической прогрессии действие сложения играет ту же роль, какую в геометрической прогрессии играет действие умножения. Эта же аналогия находится и в формуле для любого члена прогрессий: в арифметической прогрессии an = а0 + dn *), в геометрической прогрессии an = а0qn; умножению разности арифметической прогрессии d на число членов п (многократное сложение) соответствует возведение в степень п знаменателя геометрической прогрессии q (многократное умножение). Между а0 и dn действие сложения, между а0 и qn действие умножения. -------------------------------------------------------------- *) В главе I мы записывали эту формулу несколько иначе, именно так: an = а1 + d(n — 1). Здесь мы вводим один лишний член, предшествующий всем остальным, именно а0; таким обрaзом в прогрессии получается всего не п, а п + 1 членов. Точно так же и в геометрической прогрессии счёт начинается не с первого, а с нулевого члена. Такая нумерация членов удобнее, потому что число последовательных операций (сложений—в случае арифметической, умножений—в случае гчометричeской прогрессии) получается равным п, а не п — 1, что заметно упрощает формулы -------------------------------------------------------------- Тесную связь между арифметической и геометрической прогрессиями можно иллюстрировать следующим примером. Рассмотрим геометрическую прогрессию, у которой а0 = 2; q = 1,2. Вычисления дают: а0 = 2; а1 = 2,4; а2 = 2,88; а3 = 3,46; а4 = 4,15; а5 = 4,98, ... Строим оси координат и график гиперболы у = 1/x (черт. 28).
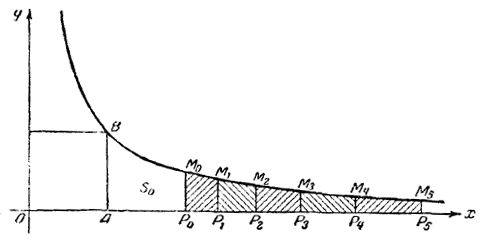
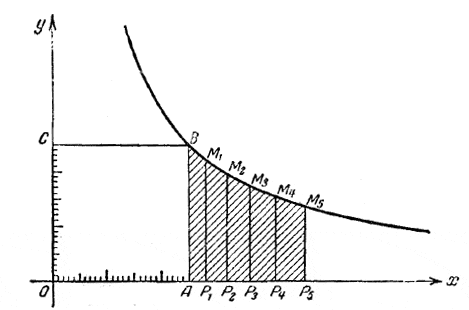
Черт. 28 Вдоль оси Ох откладываем от начальной точки О последовательно отрезки: ОА = 1; ОР0 = 2; ОР1 = 2,4; ОР2 = 2,88; ОР3 = 3,46; ОР4 = 4,15; ОР5 = 4,98. В концах этих отрезков строим ординаты точек гиперболы. Мы получим криволинейную фигуру АР0М0В и ряд криволинейных фигур Р0Р1М1М0, P1Р2M2M1, Р2Р3М3М2 Во второй главе было доказано, что величина площади таких фигур не зависит от длины отрезков [а1 ... а2], [а2 ... а3] и т. д., но только от отношений
А потому можно утверждать, что все указанные площади (за исключением первой) равны между собой: пл. Р0Р1М1М0 = пл. P1Р2M2M1 = пл. Р2Р3М3М2 = ... = S. Площадь первой фигуры АР0М0В обозначим S0. Отсюда получаем площадь на отрезке [1 ... а0] = S0 Таким образом площади, опирающиеся на эш отрезки, составляют арифметическую прогрессию, в то время как длины отрезков ОР0, OP1, ОР2, ОР3,... образуют геометрическую прогрессию. Этим мы установили связь между обеими прогрессиями. Рассмотрим ещё геометрическую прогрессию, у которой начальный член а0 = 1: 1, q, q2, q3 ,q4, ... Пусть, например, q = 1, 2. Если для этой прогрессии построить график (черт. 29), такой как для предыдущей, то получим ряд равных между собою площадей:
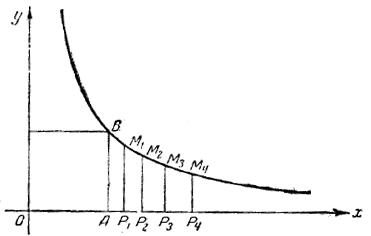
Черт. 29 Получаем: площадь на отрезке [1 ... l ] = O. И здесь имеет место соответствие между геометрической прогрессией Свя:ь между геометрической прогрессией длин отрезков и арифметической прогрессией площадей можно формулировать cлeдующим образом: возвышению в степень длины отрезка q соответствует умножение площади S0 на число п. Шестое действие арифметики. Как уже отмечалось в первой главе, действие, обратное возвышению в степень, называется извлечением корня. Если, например, 27=128, т. е. 2, умноженное на себя 7 раз, даёт в результате 128, то можно написать: 2 = 7√128. Если x4 = 52, то х = 4√52. На практике часто приходится решать задачи, приводящие к извлечению корня. Рассмотрим задачу, для решения которой применим наши познания о геометрической прогрессии. Автомобильный завод в 1945 г. выпускал ежедневно 200 машин. По плану четвёртой пятилетки он должен довести в 1950 г. ежедневный выпуск до 360 машин. Спрашивается: как следует ежегодно повышать выпуск продукции, чтобы процент повышения по отношению к предыдущему году оставался одним и тем же? Мы знаем, что в этом случае выпуск машин по годам составит геометрическую прогрессию ( пример в начале главы). Годы ........ 1945 1946 1947 1948 1949 1950 Выпуск машин а0 а0q а0q2 а0q3 а0q4 а0q5 Нам известно при этом, что а0 = 200, а0q5 = 360. Задача заключается в том, чтобы определить q (коэффициент ежегодного увеличения). Из написанных равенств следует q5 = 360/200 = 1,8, следовательно, q = 5√1,8. Но знак корня мало помогает делу. Надо уметь его извлечь (вычислить). Паскаль по этому поводу справедливо заметил, что поставить новый математический значок—это всё равно, что приклеить новый ярлык, но этим ещё не разрешается задача. Ведь для вычисления корня пятой степени мы не имеем никаких средств. Недаром в течение многих веков эта задача считалась неразрешимой. Средство для её решения было найдено только в 1614 г., когда шотландский математик Джон Непер опубликовал свои «удивительные таблицы» логарифмов. Мы же решим эту задачу без помощи логарифмов, пользуясь знакомой нам гиперболой (черт. 30).
Черт. 30 Чертёж надо сделать в крупном масштабе на миллиметровой бумаге. Отложим на оси Ох отрезок ОА = 1 и отрезок ОР5 = 1,8. Если бы на оси Ох были отложены отрезки OP1= q, ОР2 = q2, OP3 = q3, OP4= q4, то площади, построенные на отрезках AP1 , Р1Р2 , Р2Р3, Р3Р4, Р4Р5, должны быть равны между собой. пл. AP1M1В = пл. P1Р2M2M1 = пл. Р2Р3М3М2 = пл. P3Р4M4M3 = пл. Р4Р5М5М4 = S Вся площадь АР5М5В была бы равна 5S. Чтобы определить площадь АР5М5В подсчитаем число миллиметровых квадратиков сетки, заключённых в пределах этой фигуры. Для получения более точного результата следует учесть число квадратиков, пересечённых дугой гиперболы, считая каждый за половину. Подсчёт покажет, что в криволинейной площади АР5М5В содержится приблизительно 380 квадратиков. Эти 380 квадратиков составляют 5S; следовательно, S содержит приблизительно 380/5 квадратиков, т. е. около 76 квадратиков. Теперь остаётся только провести ординату P1M1 с таким расчётом, чтобы площадь AP1M1В содержала 76 квадратиков. После этого надо измерить длину отрезка OP1, которая даёт искомую величину q. Она равна приблизительно 1,12. Значит, автомобильный завод должен ежегодно повышать выпуск продукции на 12%. Конечно, этот способ неточный и громоздкий, однако, он передаёт идею того, как математики справлялись с задачей извлечения корня, т. е. преодолевали трудность шестого действия арифметики. Позднее будет показано, как составить таблицу, дающую для каждого отрезка ОР = х величину соответствующей криволинейной площади АРМВ, лежащей над отрезком [1...х]. Имея такую таблицу, уже нет надобности подсчитывать квадратики. Вопросу о составлении таких таблиц (таблиц логарифмов) будет посвящена пятая глава этой книги *). ----------------------------------------------- *) Заметим, что в XVII веке были изобретены и другие способы вычисления корней любой степени, например, с помощью рядов. Но для повседневной практики наиболее удобно вычисление с помощью логарифмов. |