ГЛАВА IV.

АРИФМЕТИЧЕСКИЙ ТРЕУГОЛЬНИК ПАСКАЛЯ.

2. Таблица Тартальи.

Пусть дан ряд чисел:

21,   56,   126,   252,   462,    792,   1287,   2002.

Если спросить, взяты эти числа случайно или по какому-то определённому правилу, то на этот вопрос ответить будет нелегко. Оказывается, для данного ряда такое правило имеется, но оно глубоко скрыто. Мы его вскроем следующим образом.

Найдём разности между соседними числами; получим ряд:

35, 70, 126, 210, 330, 495, 715.

Для этого ряда найдём опять разности между соседними числами; получим:

35, 56, 84, 120, 166, 220.

Будем продолжать этот процесс нахождения разностей. Получим ряд:

21, 28, 36, 45, 55,

затем следующий:

7, 8, 9, 10,

т..е. ряд последовательных целых  чисел,   или   арифметическую прогрессию. Если   взять ещё раз разности, то получим ряд равных чисел

1, 1, 1.

В этом и заключается закономерность выше предложенного ряда чисел.

Все ряды разностей можно сопоставить в одной таблице:

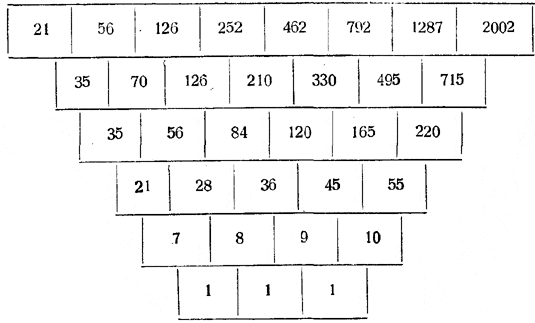
Нам придётся решать обратную задачу, т. е. переходить от простой арифметической прогрессии к более сложным рядам. Построение таких рядов (более высокого порядка) приводит к так называемой таблице Тартальи-Паскаля.

Пусть имеются бильярдные шары в большом количестве. Будем их укладывать на плоскость в виде треугольника; из них можно составить группы, изображённые, на черт. 36: 1) из 1 шара; 2) из 3 шаров; 3) из 6 шаров; 4) из 10 шаров, и так далее.

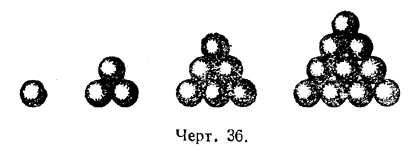
Заметим, что при образовании четвёртой группы надо было к третьей группе добавить 4 шара; при образовании пятой группы надо добавить 5 шаров и т. д. Нетрудно видеть, что число всех шаров четвёртой группы равно 1+ 2 + 3 + 4 = 10,   число    шаров   пятой   группы   равно 1+2 + 3 + 4 + 5=15.   Число   групп  шаров   с  номером т равно 1+2 + 3 +  ... + т.

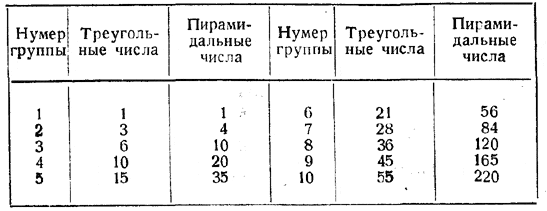
Запишем числа шаров каждой группы параллельно с числами натурального ряда (нумерами групп). Получим таблицу:

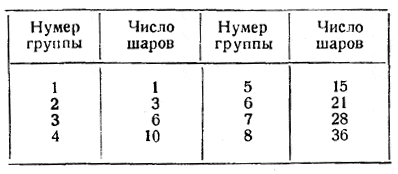
Так как составленные нами группы шаров имеют форму треугольника, то числа, стоящие с правой стороны, получили название «треугольных» чисел.

Будем теперь складывать шары в пространственные группы в форме треугольных пирамид (черт. 37).

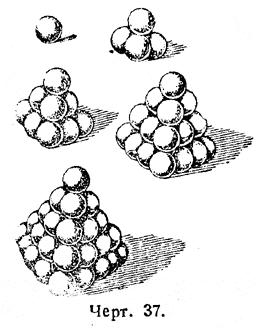
За группой из одного шара идёт такая группа: 3 шара внизу, один над ними, всего 4 шара. Более сложные группы можно получить, если накладывать друг на друга различные плоские группы. Если группу из 6 шаров положить на плоскость в форме треугольника, а плоскую группу из 3 шаров поместить в углублениях над ними, то получим как бы двухэтажную группу, добавив к которой сверху 1 шар, получим пирамиду из 10 шаров (третья пирамида — черт. 37).

Можно продолжить такое построение: надо поместить на плоскость группу из 10 шаров, опять в форме треугольника, и над этим слоем поставить всю предыдущую группу. Получим «четырёхэтажную» группу из 1 + 3 +  6 + 10 = 20 шаров. Далее, можно под предыдущую «постройку» подвести фундамент в виде плоской треугольной группы из 15 шаров. Получится группа из 1 +3 +-6 + 10+ 15 = 35 шаров и т.д. Из этого процесса построения следует, что числа шаров пространственных групп получаются путем сложения одного, двух, трёх и так далее чисел того ряда, который мы выше назвали рядом «треугольных чисел». Поэтому совсем нетрудно дополнить предыдущую таблицу ещё одним, третьим столбцом чисел. Новый ряд чисел получил название  «пирамидальных». Числа натурального ряда, треугольные и пирамидальные числа, а также числа, которые мы сейчас получим, носят название фигурных чисел.

Числа, стоящие в первом столбце нашей таблицы, назовём   фигурными   числами первого порядка; числа, стоящие во  втором столбце,— фигурными числами второго порядка; наконец, числа третьего столбца —фигурными числами третьего порядка. Мы  получили эти числа  с  помощью геометрических фигур, состоящих из шаров; но их можно получить и иначе. Верхнее число каждого столбца равно единице. Второе число получается путём сложения этой единицы с числом предыдущего столбца, стоящим во второй строке; третье число каждого столбца получается путём сложения второго числа того же столбца с третьим числом предыдущего столбца и т. д.

Хотя уже нельзя строить геометрические фигуры из шаров, числа которых давали бы числа следующего, четвёртого, столбца, однако, подмеченное нами правило даёт возможность построить эти числа: пишем в первом ряду четвёртого столбца 1; к нему прибавляем 4 (второе число третьего столбца), получаем 5 (второе число четвёртого столбца) и т. д.

Вот фигурные числа четвёртого порядка:

1, 5, 15, 35, 70, 126, ...

Ничто не мешает из полученных чисел образовать числа пятого порядка и т. д.

В пятом столбце получим ряд чисел:

21, 56, 126, 252, 792, 1287,

о которых шла речь в начале параграфа.

С левой стороны таблицы добавляется ещё один вертикальный столбец, состоящий из одних единиц; числа этого столбца (единицы) называют фигурными числами нулевого порядка. В результате получим таблицу:

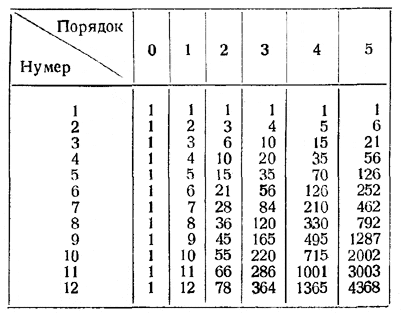
Так построенная таблица фигурных чисел впервые встречается в большом сочинении по арифметике Тартальи (1500—1557). Однако систематическое изложение свойств чисел различных порядков было дано лишь в сочинении «Об арифметическом треугольнике» Паскаля (1623-1662).

Укажем теперь на основное свойство полученной таблицы. Из самого способа её составления вытекает следующее: если взять, например, первые 10 чисел второго порядка, то их сумма равна одному десятому числу третьего порядка. Чтобы это показать, заметим, что   в третьем   столбце   второе   число   4   равно   сумме  1+3; третье число 10 равно 4+6 или же 1+3 + 6 четвёртое число 20 равно 10+10 или же 1+3 + 6+10, т. е. четвёртое число третьего столбца равно сумме первых четырёх чисел второго столбца; пятое число третьего столбца 35 равно 20+15 или же 1 + 3 + 6 +  10 + 15, т. е. сумме первых 5 чисел второго столбца, и так далее. Поэтому и десятое число третьего порядка равно сумме первых 10 чисел второго порядка. Таким же образом можно показать, что, например, сумма первых 8 чисел третьего порядка равна одному восьмому числу четвёртого порядка.

Общее правило таково: сумма первых п фигурных чисел какого-либо порядка равна одному п-му числу следующего порядка.

Введём следующие   обозначения. Число, стоящее  на т-й строке и в столбце с нумером k, обозначим через F_m^k ; например, 8-е фигурное  число  второго порядка будет обозначаться через F₈² 10-е число третьего   порядка F₁₀³  и т. д.

Тот факт, что сумма первых шести чисел второго порядка равна шестому числу третьего порядка, в этих обозначениях запишется так:

F₁² + F₂² + F₃² + F₄² + F₅² + F₆² = F₆³.

Таким образом можно записать, что сумма первых восьми чисел третьего порядка равна восьмому числу четвёртого порядка:

F₁³ + F₂³ + F₃³ + F₄³ + F₅³ + F₆³ + F₇³+ F₈³= F₈⁴.

Можно записать и общую формулу такого «автоматического» сложения:

F₁^k + F₂^k + F₃^k+...+ F_{n — 1}^k+ F_n^k =  F_n^k+1        (1)

Если бы мы имели в своём распоряжении весьма большую таблицу, то могли бы сразу находить суммы такого рода; например, сумму первых 300 чисел третьего порядка; сумму первых 450 чисел четвёртого порядка и т. д.

Но оказывается, можно производить такое суммирование сразу, не имея огромных таблиц. Можно, например, быстро найти сумму первых 300 слагаемых третьего порядка без таблицы. Для этого, согласно изложенному, достаточно знать только фигурное число F₃₀₀⁴.  Но как его узнать? Ответ на этот вопрос даёт формула другого математика Пьера Ферма (1601 —1665). Эта формула впервые встречается в письме, которое Фермa писал своему приятелю в 1636 г., т.е. более трёхсот лет назад. Фигурное число  F₃₀₀⁴, согласно формуле  Фермa,   равно

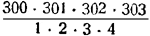
К выводу формулы Фермa  мы и перейдём.