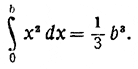|
ГЛАВА VI. КЛЮЧ МЕРКАТОРА. Целью настоящей главы является вывод формулы, позволяющей вычислить логарифм какого угодно числа с любой степенью точности. Формулу эту впервые вывел Меркатор (вывод её будет дан в §§ 3 и 4 настоящей главы). Однако этот вывод не возможен без предварительного знания другой формулы, которая была известна задолго до Меркатора. Она играет исключительно важную роль в математике и во всех её приложениях (в механике, физике и т. д.). Эта формула явилась результатом продолжительной работы многих учёных XVI века, которые с различных сторон подходили к её выводу. Среди этих учёных следует отметить имена Галилея, Кавальери, Фермa, Паскаля, Кеплера, Валлиса. Сейчас мы имеем возможность вывести её весьма просто, если воспользуемся формулами для Σk (суммы степеней чисел натурального ряда), полученными в I и IV главах. Так мы и поступим в § 2 настоящей главы. Но чтобы дать представление читателю о тех крайне извилистых путях, которыми различные учёные шли к её нахождению, мы предварительно в §1 рассмотрим вывод этой формулы, принадлежащий Кавальери (1591 (?) — 1647 г.) 1. «Неделимые» Кавальери. Кавальери думал, что площадь любой плоской фигуры, например, площадь параллелограмма, можно представить себе составленной из бесчисленного множества тончайших линий, приложенных одна к другой. Эти линии настолько тонки, что дальше их делить невозможно, и потому их назвали «неделимыми». Добавим, что Кавальери аналогично этому представлял себе, что прямая линия может быть составлена из бесчисленного множества точек; что фигурa трёх измерений может быть составлена из бесчисленного множества плоских фигур. В настоящее время мы знаем, что такая точка зрения является неправильной. Однако в этом параграфе мы рассмотрим, как Кавальери, пользуясь этим неправильным представлением, пришёл к весьма важному и правильному результату, а именно, определил значение интеграла Теорема: «Пусть дан параллелограмм AEGC и в нём проведена диагональ ЕС. Тогда «все квадраты» *) параллелограмма относятся ко «всем квадратам» треугольника АЕС, как 3:1». *) Под словами: «все квадраты» Кавальери подразумевает сумму квадратов длин линий, из бесчисленного множества которых составляется площадь параллелограмма.
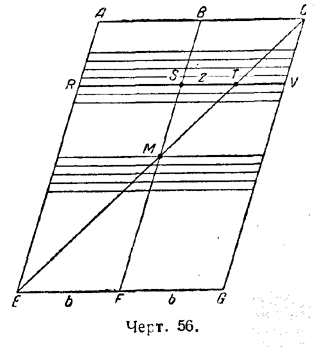
Пусть параллелограмм AEGC (черт. 56) получается путём последовательного приложения (суммирования, сложения) бесчисленного множества тончайших линий одной к другой, например, линий, равных и параллельных АС. Таких линий может быть сотни тысяч, миллионы и т. д. Берём теперь сумму квадратов длин этих линий. Теоремой утверждается, что сумма квадратов всех этих линий, составляющих параллелограмм, относится к сумме квадратов всех «составляющих» линий треугольника АЕС или треугольника ECG, как 3:1, или, обозначая сумму квадратов длин этих прямых через греческую букву Σ, имеем, согласно теореме, что Σ (AEGC) = 3Σ (AEC). Для доказательства теоремы делаем дополнительное построение: проводим прямую линию BF, где В —середина AC, F — середина EG. Пусть RV — одна из прямых, параллельных АС. Прямая RV делится диагональю ЕС на две части: RT и TV. Пусть RТ = х, TV= y, AC = a, АВ = 1/2 a= b, ST = z. Тогда RT= RS + ST = b + z, TV = b — z. При движении прямой RV сверху вниз, до точки М, RT больше TV, ниже точки М —наоборот: TV больше RT. Для доказательства своей теоремы Кавальери пользуется следующим тождеством: RТ2 + ТV2 = х2 + у2 = ( b + z )2 + (b — z)2 = 2b2 + 2z2. х2 + у2 = 2b2 + 2z2. (1) Это равенство (1), справедливое для любого отдельного положения прямой RV, Кавальери «суммирует» для «всех» возможных её положений при движении её сверху вниз, от положения АС до положения EG. Выражаясь грубо, если таких положений прямой, таких ниток, из которых «соткана» площадь параллелограмма, будет, например, миллион, то он складывает миллион слагаемых слева и миллион слагаемых справа: Σ х2 + Σ у2 = Σ 2b2 + Σ 2z2. (2) Результат суммирования Σ х2 «всех» квадратов и есть искомая величина, которую обозначим через [АЕС] или Вторая сумма Σ у2, т. е. сумма квадратов хорд TV, или [ECG], очевидно, равна предыдущей сумме [AЕС]. Итак, в левой стороне равенства (2) имеем 2 [АЕС] = 2 Σ b2 = Σ 1/4 a2 = 1/4 Σ a2 = 1/4 [AEGC] Перейдём теперь к суммированию Σ z2 произведённому вдоль всей высоты АЕ. Нетрудно видеть, что в результате получится сумма квадратов хорд ST внутри треугольника ВМС плюс такая же сумма внутри треугольника EMF. Ввиду симметрии указанных двух треугольников, две последние суммы квадратов равны. Сравним теперь [ВМС] с основной суммой [AEС] =
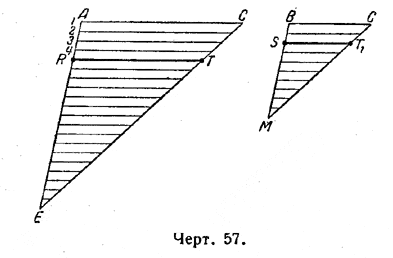
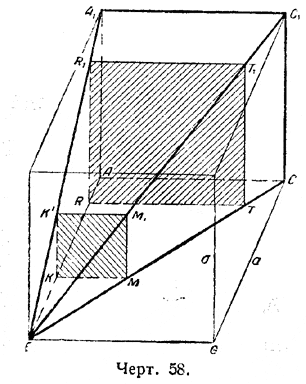
Каждая хорда меньшего треугольника AЕС в два раза меньше соответствующей хорды большего треугольника AEC: S1T1 = 1/2 RT; квадрат меньшей хорды (S1T1)2 в 4 раза меньше квадрата соответствующей хорды большего треугольника (RT)2. Сверх того, если расстояния между соседними хордами брать одинаковыми у обоих треугольников, то и число хорд у меньшего треугольника будет в 2 раза меньше числа хорд большего треугольника *). *) Не следует забывать, что хорды, о которых идёт речь, являются «неделимыми». При счёте с этими неделимыми следует соблюдать особую осторожность, чтобы не сделать при этом ошибки. В результате «сумма всех квадратов» хорд треугольника ВМС в 8 раз меньше «суммы всех квадратов» хорд треугольника АЕС. Подведём итог суммирования левой и правой части основного равенства: Σ х2 + Σ у2 = 2 Σ b2 + 2 Σ z2 Имеем, согласно введённым обозначениям: 2 [АЕС] = 2 [AEFB] + 2 [ВМС] + 2 [EMF], или 2 [АЕС] = 2 • 1/4 [AEGC] + 4 [ВМС], или 2[AEC] = 1/2[AEGC] + 41/8 [АЕС], или 2 Из этого равенства определяем искомое 3/2 откуда окончательно i 1/2 = [AEC] = 1/3[AEGC]. Полученный результат можно пояснить на следующей пространственной модели (черт. 58).
Для простоты, заменим основной параллелограмм AEGC квадратом со стороной а. Представим себе, что в треугольнике ЕАС проведено множество равноотстоящих, параллельных между собой, отрезков RT (параллельно АС). На каждом из этих отрезков строим квадрат RR'T'T, лежащий в плоскости, перпендикулярной к плоскости ЕАС. Вершины R' и Т' этих квадратов будут лежать соответственно на прямых ЕА' и ЕС'. По идее Кавальери «сумма всех» этих квадратов, т. е. сумма величин второго измерения, даёт объём пирамиды ЕАА'С'С, т. е. величину третьего измерения. Эта «сумма» выше нами была обозначена через [ЕАС]. Сделаем такое же построение для отрезков типа RV в квадрате EAGC; все эти отрезки должны быть параллельны (и равны) АС. Нетрудно видеть, что «сумма всех» квадратов RR'V'V даст, по идее Кавальери, объем куба EACGE'A'C'G'; объём этот численно равен а3. Таким образом, теорема Кавальери утверждает, что объём пирамиды с основанием АА'С'С и высотой ЕА равен трети куба с тем же основанием и равной высоты. В настоящее время содержание теоремы Кавальери и соответствующей теоремы из учебника геометрии лучше всего может быть выражено формулой интегрального исчисления:
|
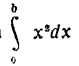(не используя, разумеется, самого понятия интеграла, которое было придумано позже).
