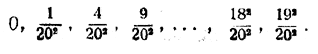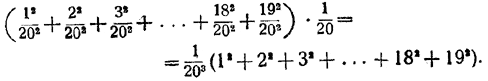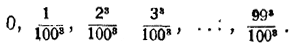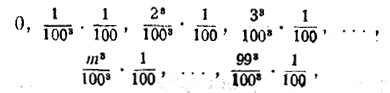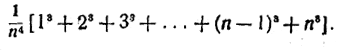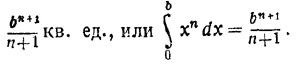ГЛАВА VI.

КЛЮЧ МЕРКАТОРА.

2. Площадь «под» параболой.

Рассмотрим выражение х² . Если х означает переменное количество, то и величина    х² будет переменной. Если х получает последовательно значения 1, 2, 3, 4,... , то х² будет принимать значения 1, 4, 9, 16,.., Переменному х можно давать и промежуточные значения, например: 1;  1 ¹/₂ ; 2; 2¹/₂ , 3, ... ; тогда х² будет соответственно равен 1; 2¹/₄; 4; 6 ¹/₄ ; 9,...

Обозначим х² через у, т. е. положим у = х². Значения переменных х и у можно расположить в виде прилагаемой таблицы:

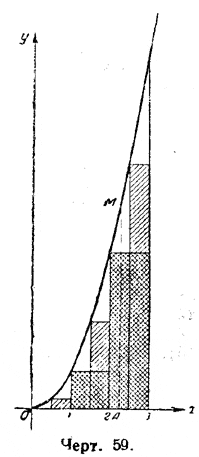
Если считать, что переменное х изменяется непрерывно и, возрастая, принимает последовательно все возможные числовые значения, то у будет изменяться также непрерывно. Связь между обеими переменными удобно представить графически (черт. 59).

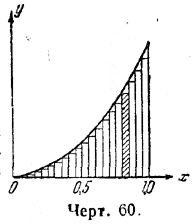
Если х непрерывно возрастает, то точка А —конец отрезка ОА, изображающего число х,—движется по оси Ох вправо, постепенно удаляясь от точки О. Если для каждого значения х (для каждого возможного положения точки А) построить ординату AM, равную соответствующему значению у, то концы этих ординат будут лежать на плавной кривой линии, называемой параболой; так как х² есть вторая степень от х, то эту параболу называют также параболой второй степени.

Пусть на чертеже имеется парабола у = х². Задача, которую мы теперь хотим решить, состоит в определении площади, ограниченной отрезками ОА и AM и криволинейной дугой параболы ОМ (площади «под» параболой).

В течение многих веков учёные пытались решить задачу об определении площадей, ограниченных некоторыми кривыми линиями, но их попытки оставались безуспешными. Некоторые удачные результаты получил древнегреческий математик Архимед, но в позднейшие века произошёл застой в развитии математики, и даже приёмы Архимеда были  забыты.  Новое оживление  наступило в XVI и XVII веках, когда начала зарождаться так называемая высшая математика. В исследованиях учёных того времени —Кеплера, Валлиса, Ферма, Паскаля, Барроу, Лейбница, Меркатора, Маклорена и других — определение площадей и объёмов, ограниченных кривыми линиями и поверхностями, занимало центральное место. Трудность этой задачи состоит в том, что кривая линия, ограничивающая площадь, искривлена даже в своих мельчайших частях, а потому такую площадь нельзя разбить на треугольники, прямоугольники и другие фигуры, ограниченные прямыми линиями. Пробовали найти выход  в том, чтобы мысленно разделить площадь на «бесконечное» множество полосок, как это делал Кеплер, или пользовались «неделимыми», как Кавальери, но эти рассуждения с бесконечностями отличались крайней туманностью, и математика была вынуждена от них отказаться.

Правильное решение вопроса было найдено тогда, когда отказались от лобовой атаки и пошли обходным путём. Ключ к разрешению задачи для параболы второй степени дала выведенная нами формула для Σ₂

Решим задачу сперва для случая, когда отрезок на оси Ох есть [0... 1]. Разделим этот интервал (черт. 60) на некоторое   число  равных долей, например, на 20, и построим ординаты у для значений х : 0, ¹/₂₀ ,  ²/₂₀ , ³/₂₀ , ... , ¹⁸/₂₀ , ¹⁹/₂₀ . 

Длина соответственных ординат у будет:

Построим ступенчатую фигуру, как  показано  на чертеже.

 Ширина каждой прямоугольной полоски равна ¹/₂₀ ед. Площадь полоски с нумером т будет равна: . Площадь всей ступенчатой фигуры будет равна:

Если отрезок [0 ... 1] на  оси Ох разделим на большее число  равных долей,   например   на 100 (п =100), то получим для площади  ступенчатой фигуры значение

Но,   очевидно,   при  увеличении числа  долей n, величина   площади ступенчатой   фигуры   делается   все ближе и ближе к искомой криволинейной площади. Это ясно виднс на черт. 59, на  котором заштрихованная в клетку площадь есть площадь ступенчатой фигуры при п = 3, а площадь всей заштрихованной  фигуры есть площадь ступенчатой фигуры при п = 6.

Если допустить, что число долей п растёт неограниченно, и если при этом величина площади ступенчатой фигуры

будет приближаться к некоторому постоянному числу, то это предельное число и даст искомую площадь криволинейной фигуры. Но как сосчитать сумму квадратов, если взять п =1000; п = 10000 и так далее? Формула Для Σ₂ дает выход из этого затруднения.

Чтобы удобнее было применить формулу для Σ₂, добавим к выражению,   стоящему в скобках, ещё одно слагаемое п². От этого сумма увеличится на величину ; если же п неограниченно возрастает, то величина дроби ¹/_n стремится к нулю, а потому результат от прибавления этой дроби в пределе не изменится. Получим выражение:

Но мы имели

Поэтому площадь ступенчатой фигуры вместе с дополнительным слагаемым ¹/_n равна:

Если, например, взято n =1000, то площадь равна:

Если взять значение п = 10 000, то площадь будет равна:

и т. д.

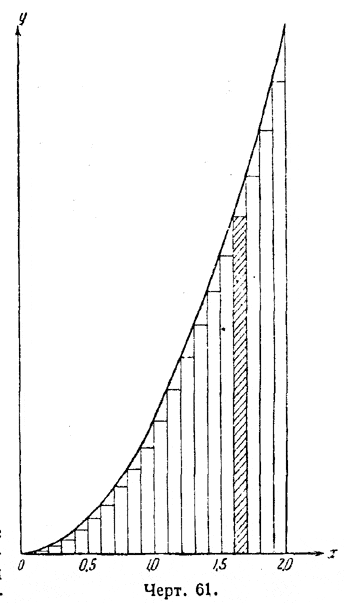
Если число п увеличивать всё больше и больше, то в выражении второе слагаемое, а тем более третье, будет приближаться к нулю, а всё выражение в целом— к постоянному числу, равному ¹/₃. Отсюда заключаем, что точная величина площади, ограниченной параболой у = х², ординатой и отрезком [0... 1], равна ¹/₃ кв. единицы.

Перейдём теперь к случаю, когда парабола взята не на отрезке [0... 1], а на большем отрезке, например, на отрезке [0 ... 2]. Мы имеем в виду перейти в дальнейшем к любому отрезку [0... b] (черт.. 61).

Сравним площадь «под» параболой на отрезке [0... 2] с площадью «под» параболой на отрезке [0 ... 1]. Будем производить с новой площадью те же операции, как с прежней. Разделим отрезок [0 ... 2] сперва на 20 равных долей, затем  на 100 долей, на 1000 долей и т. д. и будем делать одновременно  то же самое с прежней площадью   на    отрезке[0... 1].   Если оба отрезка   [0 ... 1]  и [0 ... 2]     разделены на равное число долей и построены соответствующие фигуры, то ширина полосок одного и того же нумера в обеих ступенчатых  фигурах будет различной: во второй фигуре она будет в 2 раза больше.  Высота  каждой полоски во второй фигуре будет в 4 раза больше,  чем  высота полоски с тем же нумером в первой фигуре, так как,  при увеличении х в 2 раза,   у = х²  увеличивается в 4 раза. Поэтому площадь, каждой полоски второй фигуры  будет в 8 раз больше, чем площадь соответствующей полоски первой фигуры. А так как это отношение (8:1) остаётся постоянным для  всех пар полосoк с одинаковым нумером, то и вся вторая ступенчатая   фигура в 8 раз больше первой ступенчатой фигуры. При дальнейшем увеличении числа n отношение (8:1) остаётся неизменным, поэтому точная площадь второй криволинейной фигуры также в 8 раз больше, чем точная площадь первой криволинейной фигуры (на черт. 60 и 61 эти соотношения не вполне выдержаны).

Мы взяли для второй фигуры интервал [0... 2]. Если бы мы взяли для неё интервал [0... 7], то получили бы, что её площадь больше площади на интервале [0 ... 1] в 343 раза: 7³ = 343.

Так как площадь, лежащая на интервале   [0...1],  как  мы  показали, равна ¹/₃ кв. ед., то для площади, лежащей на любом интервале [0 ... b], площадь равна ¹/₃ b³ кв. ед. Это и есть решение нашей задачи.

Таким же путём решим задачу определения площади «под» параболой у = х³, параболой третьей степени (черт. 62).

Опять-таки сначала решим задачу для интервала [0... 1]. Попрежнему делим отрезок  ОР = х на n равных долей. Если взять п =100, то последовательные значения абсциссы ОР = х будут:

а соответствующих ординат у:

Площади прямоугольных полосок будут равны:

т, е.

Вся площадь ступенчатой фигуры  окажется равной

Если  п — произвольное число,   то рассматриваемая площадь равна:

Как и раньше, заменим эту величину другой, весьма мало от неё отличающейся:

В скобках стоит сумма кубов:

Поэтому площадь ступенчатой фигуры равна:

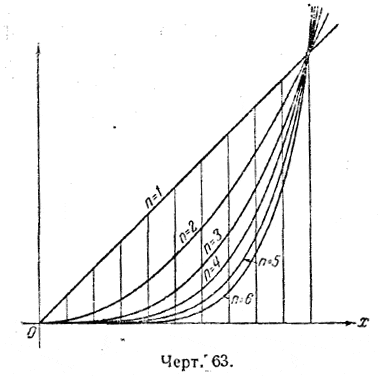
Чем больше число долей п, тем меньшую роль играют второе и третье слагаемые. При неограниченном возрастании числа п второе слагаемое, а тем более третье, стремятся к нулю. А потому искомая криволинейная площадь равна ¹/₄ кв. ед. Этот результат является уже совершенно точным.

Как и раньше, рассмотрим ещё общий случай задачи, когда отрезок на оси Ох будет не [0... 1], а какой-нибудь [0 ... b], например, [0 ... 3].

Опять сравниваем прямоугольные полоски ступенчатой фигуры на интервале [0... 1 ] с полосками фигуры, построенной на интервале [0 ... 3] при одном и том же значении  п. У второй фигуры ширина полосок в 3 раза больше, а высота в 3³ = 27 раз больше, чем у первой.   Поэтому   площади  прямоугольных  полосок у второй фигуры в 3⁴ = 81 раз больше, чем у первой. Значит, и вся площадь второй ступенчатой фигуры в 81 раз больше площади первой ступенчатой фигуры, При безграничном возрастании п обе ступенчатые фигуры переходят в конце концов в криволинейные фигуры, и для последних сохраняется отношение площадей (81 :1).

Так как площадь, связанная с параболой у = х³ и лежащая на интервале [0... 1], равна ¹/₄  кв. ед., то для площади, лежащей на интервале [0 ... b], получаем величину ¹/₄ b⁴ кв. ед.

Переходя к параболам более высокой степени (на черт. 63 изображены дуги парабол   у = хⁿ на интервале [0... 1] при разных значениях п, например у = х⁴ , у = х⁵,...,) можно теперь без колебаний утверждать, что площадь «под» параболой у = х⁴ на интервале [0 ... b] равна ¹/₅ b⁵ кв. ед.; площадь «под» параболой у = х⁵ на том же интервале  равна ¹/₆ b⁶  и т. д.

Теорема:   Площадь «под» кривой у = хⁿ на интервале [0 ... b]   равна

 Эту формулу мы в дальнейшем будем называть формулой Валлиса, в сочинении которого (1655 г.) она была оригинальным образом доказана и обобщена для случая дробного показателя.