|
ГЛАВА VI.
КЛЮЧ МЕРКАТОРА.
3. Меркатор находит ключ.
Как было выше указано, задачей настоящей главы является вывод формулы, дающей возможность находить логарифмы быстро и с любой степенью точности.
Положение таково. С одной стороны, логарифм есть величина площади, ограниченной гиперболой и некоторыми прямыми, и у нас нет никаких средств подсчёта такой криволинейной площади, если не считать кустарного и неточного подсчёта клеточек на миллиметровке. С другой стороны, мы имеем последовательный ряд парабол у = х2, у = х3, у = х4,... и так далее.
К этому ряду для полноты добавляют ещё параболу 1-й степени, т. е. прямую у = х и параболу нулевой степени у = х0= 1 = const, (см. черт. 64).
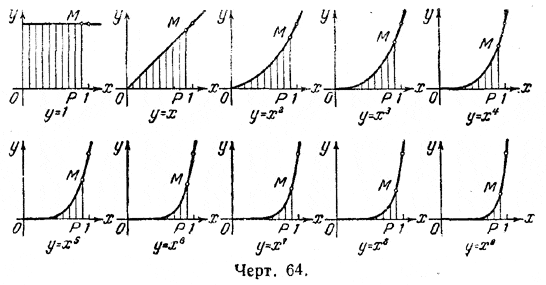
Для каждой из этих парабол мы, благодаря доказанной формуле Валлиса, умеем быстро и абсолютно точно определить величину криволинейной площади на участке [1 ... b]. Отсюда естественно является мысль: нельзя ли свести задачу о площади «под» гиперболой к задаче о площади «под» параболой?
Около 1686 г. математику Николаю Меркатору из Голштинии случайно удалось, путём несложного преобразования, найти естественное решение этой задачи *).
*) И до Меркатора было известно несколько решений задачи о площади «пол гиперболой», но все они были сложны и искусственны.
На черт. 65 имеем гиперболу, график функции у = 1/x .
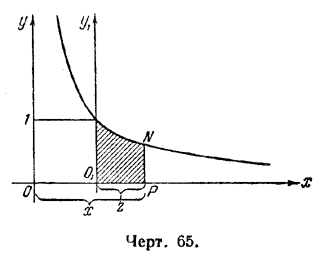
Теперь, оставляя ось Ох прежней, перенесём ось Оу на единицу вправо в положение О1у1. Если точка N, взятая на гиперболе, имела раньше абсциссу ОР = х, то новая абсцисса будет О1Р- обозначим её через z. Тогда z = x — 1 или же х = 1 + z. Уравнение нашей линии (гиперболы) у = 1/x принимает
вид: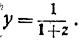 . Если, например, ОР = 1,8 ед., и искомый логарифм был выше обозначен как . Если, например, ОР = 1,8 ед., и искомый логарифм был выше обозначен как 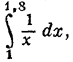 , то теперь мы должны его обозначить как , то теперь мы должны его обозначить как 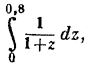 , так как новая абсцисса z изменяется, от значения 0 до значения 0,8. И вот Меркатор (в этом решающий шаг!) привлекает формулу суммы убывающей геометрической прогрессии.
А именно, мы знаем из III главы, что: , так как новая абсцисса z изменяется, от значения 0 до значения 0,8. И вот Меркатор (в этом решающий шаг!) привлекает формулу суммы убывающей геометрической прогрессии.
А именно, мы знаем из III главы, что:
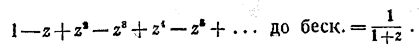
Казалось бы эта формула нужна для того, чтобы сложное выражение бесконечной суммы преобразовать в простое, стоящее справа. Меркатор же, наоборот, заменяет простую дробь 1/1+z бесконечным знакопеременным рядом, расположенным по степеням буквы z. Он получает:
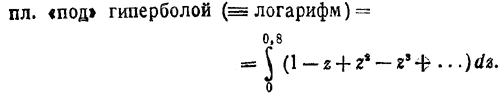
Стоящий справа знак интеграла, как мы уже знаем, означает площадь, а уравнения
у = 1, у = —z, у = z2, у = —z3, ...
означают параболы последовательных степеней. Итак, «ключ» Меркатора, который он применил для открытия незнакомой замкнутой шкатулки — это замена площади гиперболы рядом площадей последовательных парабол.
Во времена Меркатора формула площади для параболы 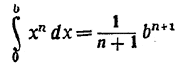 была уже хорошо известна. Что же касается того, что ряд парабол тянется неограниченно далеко (до бесконечности), то Меркатор об этом мало беспокоился. Примерно через 150 лет после него математикам стоило многих трудов доказательство того, что при этом переходе сразу к несметному множеству площадей парабол мы не совершаем ошибки, одним словом, логически-строгое
доказательство далось нелегко. Но в ту эпоху, когда жил Меркатор, так же как и юным читателям этой книги, можно было не входить в эти тонкости и беззаботно попеременно прибавлять и вычитать площади последовательных парабол: была уже хорошо известна. Что же касается того, что ряд парабол тянется неограниченно далеко (до бесконечности), то Меркатор об этом мало беспокоился. Примерно через 150 лет после него математикам стоило многих трудов доказательство того, что при этом переходе сразу к несметному множеству площадей парабол мы не совершаем ошибки, одним словом, логически-строгое
доказательство далось нелегко. Но в ту эпоху, когда жил Меркатор, так же как и юным читателям этой книги, можно было не входить в эти тонкости и беззаботно попеременно прибавлять и вычитать площади последовательных парабол:
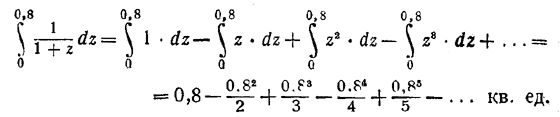
Эти последовательные площадки под параболами у = z0, у = z1, у = z2, у = z3, ..., у = z9 можно видеть на черт. 64. Конечно, значение z = 0,8 взято лишь в качестве примера. Можно написать в общем виде:
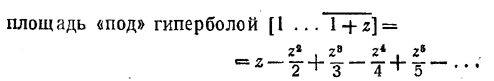
Но слева мы имеем, согласно определению в конце V главы, log (1 +z). Окончательная формула такова:
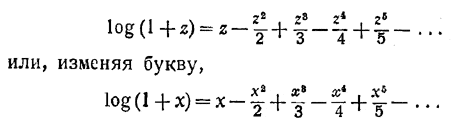
Весьма полезно будет продумать и геометрическую сторону вывода. На черт. 66 показано, каким образом происходит графическое «сложение» парабол.
Пусть, например, у(2) означает сумму у0 — у1 + у2 = 1 — х + х2;
аналогично у(3) = у0 — у1 + у2 — у3 = 1 — х + х2— х3;
итак далее.
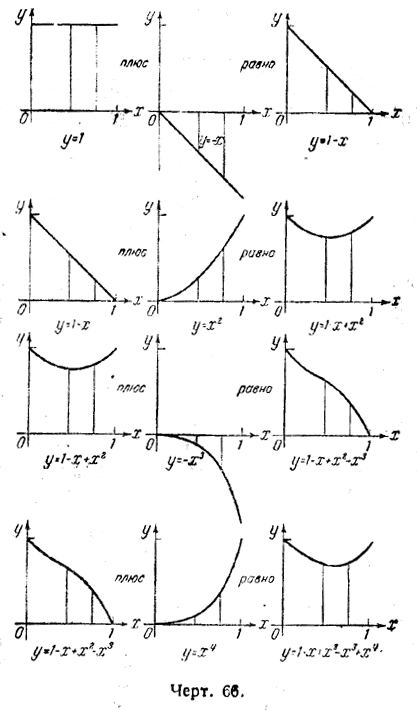
Рекомендуем читателю, пользуясь чертежом, проследить и убедиться, что площадь «под» суммарной кривой у(3) равна алгебраической сумме:
+ пл. «под» кривой (у =1),
— пл. «под» кривой (у = х),
+ пл. «под» кривой (у = х2),
— пл. «под» кривой (у = х3).
Путём последовательного прибавления всё новых и новых парабол можно добиться того чтобы суммарная парабола у(n) на всём протяжении отличалась от гиперболы сколь угодно мало.
И если дробь 1/1+x есть предел суммы ряда 1 — х + х2 — х3 + х4 — ... при неограниченном увеличении числа слагаемых, то в геометрической модели можно, путём накапливания всё новых и новых парабол, получить кривую, почти совпадающую с гиперболой.
Коротко выражаясь: гипербола есть предельная кривая при графическом сложении парабол, когда п —> ∞.
При этом, однако, следует сделать оговорку, что значение х должно быть меньшим чем 1, так как мы умеем находить сумму (точнее — пререл суммы) лишь для убывающей прогрессии, когда знаменатель прогрессии q = х < 1.
Заметим ещё, что расхождение между суммарной кривой у(n) и гиперболой увеличивается, если вдоль оси Ох передвигаться вправо, и оно больше всего у правого конца интервала [0 ... х]. Но можно доказать, что если отброшен хотя бы мельчайший отрезок в правом конце интервала [0 ... 1], например, если взять интервал [0 ... 0,99] или [0 ... 0,9995], то можно расхождение между у(n) и гиперболой сделать сколь угодно малым, если только взять вчисло п парабол достаточно большим.
Весьма интересным является вопрос: что же происходит, если, передвигаясь вправо вдоль оси Ох, подойти вплотную к краевой точке х =1?
В правой части равенства
1/1+x = 1 — х + х2 — х3 + х4 — х5 + ...
последовательные суммы sn будут попеременно давать 0 или 1. Геометрически это означает, что правый конец суммарной кривой у(n) будет совершать колебания (0<—>1), т. е. предела у(n) при х =1 не существует. В левой части равенства мы получаем попросту «среднее» значение 1/2 . Получается разрыв между левой и правой частью равенства.
Современная математика уделяет много внимания и таким необычным «разрывным» функциям. Нам проще всего будет отказаться от небольшой частицы в правом конце интервала, т. е. взять, например, вместо [0 ... 1] интервал [0 ... 0,999].
Итак, если считать, что х означает правильную дробь, то можно свободно пользоваться формулой Меркатора.
Имеем, например:
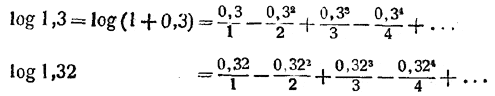
и т. д.
Покажем, как, пользуясь этой формулой, можно сравнительно быстро составить таблицы логарифмов. Сама формула
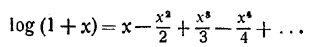
удобна только для вычисления логарифмов чисел, близких к единице, например, для вычисления log 1,01; log 1,05; log 1,1 и тому подобных. Если мы захотим вычислить логарифмы целых чисел: log 2, log 3 и т. д., то формулу Меркатора придётся немного преобразовать.
Совершенно такими же рассуждениями, как формула для log ( l + x), выводится формула и для log (1 — х). Вот эта формула:
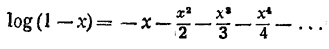
Нас не должно удивлять, что получилось выражение, имеющее при положительном х отрицательное значение: ведь при положительном х разность 1— х меньше единицы, а логарифмы чисел, меньших единицы, отрицательны.
Вычтем теперь последнее соотношение из соотношения Меркатара:
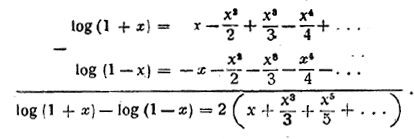
Заменяя разность логарифмов логарифмом частного, получим необычайно важную в практическом отношении формулу:
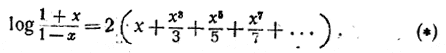
Разумное применение этой формулы требует некоторой сообразительности. Чтобы найти логарифмы целых чисел первого десятка, мы найдём сперва логарифмы двух дробей: 3/2 и 4/3 .
Каков должен быть х в формуле (*), если нужно вычислить log 3/2 ? Его легко найти из уравнения:
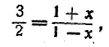
откуда х = 1/5 . Итак:
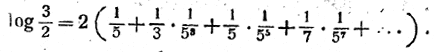
Вычислим логарифм с 10 верными знаками. Для этого в промежуточных вычислениях будем брать 12 верных знаков. Для упрощения выкладок в каждом слагаемом умножим числитель и знаменатель на 2 в той степени, в которой пятёрка входит в знаменатель этого слагаемого. Получим:
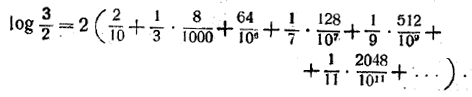
Вот что дают простые вычисления, требующие никак не больше получаса:

Во всех промежуточных вычислениях мы сохраним 12 знаков, хотя последний может быть и неверен: сами члены вычислены приближённо, а сложение приближённых чисел ведёт к увеличению возможной ошибки. Кроме того, мы отбросили длинный «хвост»; впрочем слагаемые этого «хвоста» убывают быстрее, чем члены геометрической прогрессии со знаменателем 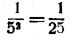 и первым членом и первым членом 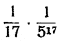 , а сумма этой прогрессии так мала, что и нa двенадцатый знак результата не может оказать, влияния. , а сумма этой прогрессии так мала, что и нa двенадцатый знак результата не может оказать, влияния.
Теперь вычислим log 4/3 . Здесь мы получим ряд, члены которого убывают значительно быстрее, чем у предыдущего. Для вычисления с 12 верными знаками в этом случае достаточно взять всего 6 членов. Правда, знаменатели здесь будут не такие «круглые», как в предыдущем примере, так что на вычисление потребуются те же полчаса.
Находим х из уравнения 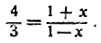 Получаем х = 1/7. Следовательно: Получаем х = 1/7. Следовательно:
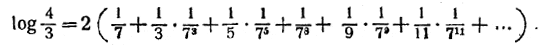
Далее располагаем действия, как в предыдущем примере:

Имея log 3/2 и log 4/3 находим сразу log 2: именно 2 = 3/2• 4/3; следовательно,
log2 = log3/2 + log4/3
Выполняем сложение:

Благодаря тому, что мы выполняли ряд действий над приближёнными числами, мы могли накопить ошибки. За 10 верных знаков после запятой можно ручаться во всяком случае:
log 2 = 0,693 147 180 6.
Пoпутно получаем логарифмы чисел 3, 4, 6, 8 и 9:
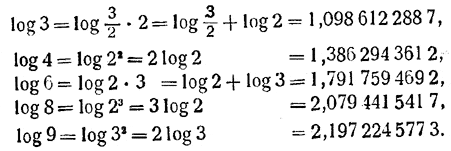
Чтобы вычислить log 5, лучше всего предварительно вычислить log 81/80. В этом случае х = 1/161 и для получения верных 12 знаков достаточно взять 3 члена ряда:
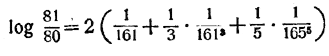 (12 верных знаков). (12 верных знаков).
Вычисление даёт:
log 81/80 = 0,012 422 519 998.
Но с другой стороны:
log 81/80 = log 34 — log 5 • 24 = 41og 3/2— log 5,
откуда
log5 = 41og 3/2— log 81/80.
Логарифм числа 3/2 был вычислен нами выше; log 81/80 мы сейчас нашли. Простая выкладка даёт:
log 5= 1,609 437 912 4 (сохраняем 10 знаков).
Прибавив log 2, найдём log 10:
log 10 = 2,3025850930 (10 знаков).
Насколько всё это проще остроумных, но утомительных вычислений Непера и Бригга!
До сих пор речь шла о вычислении натуральных логарифмов. Но мы знаем, что десятичные логарифмы получаются из натуральных простым умножением последних на постоянное число, т. е. на одно и то же число для всех логарифмов.
Но log 10 = 2,302585093 ..., a log1010 = l. Значит, чтобы получить десятичные логарифмы, нужно найденные нами натуральные логарифмы умножить на
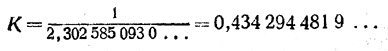
Остаётся выполнить не такие уж сложные умножения.
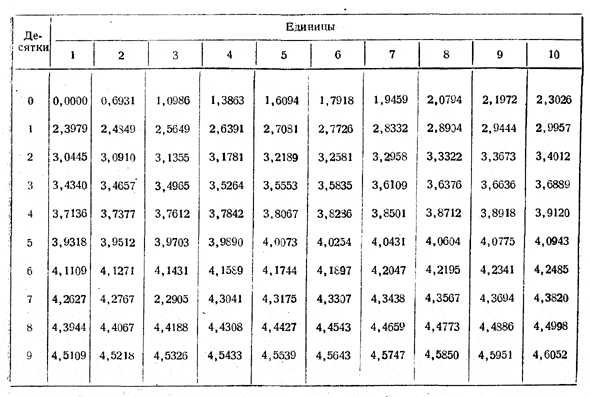
Вот четырёхзначная таблица натуральных логарифмов, которую читатель без труда мог бы составить сам, пользуясь «ключом Меркатора» .
|