|
ВАРИАНТ 1
|
|
ЧАСТЬ 1
|
|
1. Какую цифру надо вписать зместо *, чтобы число 52*1 делилось на 3?
|
|
(А) 2
|
(В) 3 |
(С) 1 |
(D) 8 |
|
2. Если формула общего члена числовой последовательности аn = (-1)n . n - 2, то член последовательности а6 равен .........................
|
|
3. Чему равен х, если 15% от х равны 3?
|
|
(А) 30
|
(В) 20 |
(С) 45 |
(D) 25 |
|
4. Дана функция y = log2x. Если  [1; 16], то наибольшее значение функции равно....... [1; 16], то наибольшее значение функции равно.......
|
|
5. Дана функция  . Вычислить . Вычислить 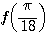 . .
|
|
(А) 
|
(В) 1/2 |
(С) 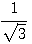 |
(D)  |
|
6. Корнями уравнения х5 - 4х3 = 0 являются............................
|
|
7. Решением уравнения 2х . 5х =100 является
|
|
(А) 3
|
(В) 10 |
(С) 2 |
(D) 1 |
|
8. Корень уравнения \/3x + 1 = 2 равен ......................
|
|
9. Решением неравенства -1 < х + 5 < 15 является
|
|
(A) x > 0
|
(B) -6 < x < 10 |
(C) x <5 |
(D) -2 < x <2 |
|
10. Найти сумму корней уравнения х2 - 4х - 3 = 0.
|
|
(А) 4
|
(В) -4 |
(С) З |
(D) -3 |
|
11. Решением неравенства log0,5 х < log0,5 7 является интервал.........................
|
|
12. На каком рисунке изображено решение неравенства sinx > 1/2?
|
 |
|
13. Сколькими способами пять человек могут встать в ряд друг за другом?.....................
|
|
14. В корзине 5 апельсинов, 3 груши и 4 яблока. Какова вероятность того, что взятый из корзины фрукт яблоко?
|
|
15. Даны векторы  и и 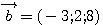 . .
Координаты вектора  равны............ равны............
|
|
16. Точка О центр окружности, вписанной в разносторонний треугольник. Какому углу равен угол 1?
|
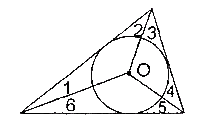 |
|
(A) / 2
|
(В) / 4 |
(С) / 5 |
(D) / 6 |
|
17. SABCD правильная четырехугольная пирамида. Проекция ребра SA на плоскость основания это отрезок.............
|
 |
|
18. ABCD - трапеция, AD = ВС, АС | ВС,
/ BAC = 30°.
/ ADC равен...........o
|
 |
|
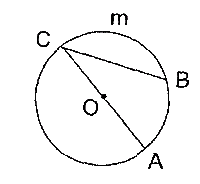
19.  BmC = 126° BmC = 126°
Вычислить величину / ACB.
|
 |
| |
| (A) 126° |
(B) 74° |
(C) 54° |
(D) 27° |
|
20. Осевое сечение цилиндра - квадрат, длина стороны которого равна 6 см. Вычислить радиус основания цилиндра.
|
|
(A) \/6 см
|
(В) 3 см |
(С) 3 см см |
(D) 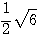 см см |
|
21. Длина спичечного коробка 5 см, ширина 3 см, площадь боковой поверхности 32 см2. Высота коробка равна..................см
|
|
ЧАСТЬ 2
|
|
1. Решить уравнение log2(x + l) + log2x = l
(6 пунктов)
|
|
2. Решить неравенство. 
(6 пунктов)
|
|
3. Школа за три месяца израсходовала на копировальные работы всю закупленную бумагу. В первый месяц израсходовали 1/5 всех упаковок бумаги, во второй месяц израсходовали на 8 упаковок больше, чем в первый месяц, а за третий месяц - 13 упаковок. Сколько упаковок бумаги израсходовали за три месяца?
(4 пунктa)
|
|
4. Боковая грань правильной четырёхугольной пирамиды образует угол 60° с плоскостью основания. Длина стороны основания равна 12 см.
Вычислить объём пирамиды.
(5 пунктов)
|
|
5. Решить систему уравнений.
(8 пунктов)
|
|
6. Решить уравнение. 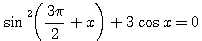
(5 пунктов)
|
|
7. При каких значениях m график функции у = (х - m)2-2 проходит через точку А(2; -1)? Построить графики с найденными значениями m.
(8 пунктов)
|
|
8. В полукруг радиуса R вписан прямоугольник так, что две его вершины находятся на полуокружности, а большая сторона прямоугольника лежит на диаметре. Отношение сторон прямоугольника равно 1 : 4 Найти площадь прямоугольника.
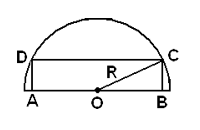 (7 пунктов) (7 пунктов)
|