Экзамен по математике. 2006 год

ВАРИАНТ I

ЧАСТЬ 1.

60 минут

Если утверждение верно, поставьте " х " в столбце "Да", если не верно, поставьте "х" в столбце "Нет"

Утверждение

 Да Нет

1.     4 • 42 = 64

    

2. 1 минута - это 1/100  часа

    

3. Число — 3,3 подходит в качестве решения неравенства х < — 5

    

4. Длина гипотенузы треугольника равна 13 см.

    
5. Диагонали параллелограмма равны    

Записать ответ в окошке напротив задания
6. Раздели      

7. Вычти   2√3  —  √3

 

 

8. Какова сумма цифр тысячей и десятков числа 3408 ?

 

 

9. Дана последовательность  . Вычисли пятый член последовательности.

 

х5 =

10. Запиши уравнение : число а в три раза больше числа b

 

а =

11. Цена товара равна Ls 120. Цену снизили на Ls 24 . Вычисли, на сколько процентов снизили цену товара.

 

 

12. Какова была скорость движения автомобиля в 13.00 ?

 

км/ч

 

13. Реши уравнение    х2 — 7х + 12 = 0

 

x1 =

x2 =

 

14. Сложи дроби

 

15. Вычисли 582 — 572

 

 

16. В спортивном лагере по утрам проходят тренировки по баскетболу, волейболу и футболу , а после обеда - по велоспорту и плаванию. Каждый участник посещает одну тренировку утром и одну - после обеда. Сколькими способами можно составить план тренировок на один день?

 

 

 

17. Определи интервал возрастания данной квадратичной функции.

 

 x с   (    ;    )

 

18. Дана функция у = х + 3 . При каком значении х функция принимает значение 10 ?

х =

 

19. Запиши в виде степени

 

20. Выполни умножение ( а — 2 )( b + 1 )

 

 

 

21. В окружность вписан правильный четырехугольник ABCD. Вычисли    

 

=       о

 

 

22. AB | | CD,  /  1 =  44о  Вычисли  /  2

 

/  2 =       о

 

 

23. Вычисли sin α

sin α =

24. Вычисли площадь параллелограмма

 

S =

 

25. /\ ABC ~ /\ DEF . Вычисли EF

EF =

 

ЧАСТЬ 2.

120 минут

1. В летнем лагере отдыхали 60 детей. Каждый ребенок назвал одно из своих любимых занятий в свободное время. Эти данные  обобщены на секторной диаграмме. На столбчатой диаграмме показан  перечень  инвентаря в лагере. 

1.1. Сколько в лагере наборов для рисования?

1.2. Вычисли, какую часть из всех детей лагеря можно обеспечить наборами для рисования.

1.3. Вычисли, сколько детей назвали бадминтон своим любимым занятием.

1.4. Дети, чье любимое занятие велоспорт, собираются в пятницу отправиться в поездку. Вычисли, сколько еще необходимо велосипедов.    (7 пунктов)

 

2. Упрости выражение (х + 2)2 + ( х + 1 ) ( 2 — х) — 2х       (4 пункта)

3. Реши систему уравнений

      (4 пункта)

4. Реши неравенство ( х + 3 )( х + 5 ) <  0

Ответ представь в виде интервала чисел       (5 пунктов)

 

5. В прямоугольной трапеции ABCD дано:

 BC = 8 см , AD = 14 см  и /  CDA = 30о

Вычислить длину отрезков CD и  AB    

(6 пунктов)

6. Велосипедист проехал 9 км за тот же промежуток, за который мотоциклист проехал 21 км. Скорость мотоциклиста на 20 км/ч больше скорости велосипедиста. Вычисли скорость велосипедиста.   

               (6 пунктов)

7. Пакет с соком имеет форму правильной треугольной призмы. Его высота равна 20 см и длина стороны основания равна 12 см.

7.1. Вычисли площадь боковой поверхности пакета с соком.

7.2. Вычисли объем пачки с соком.

7.3. Определи, можно ли в эту пачку налить 1,5 литра сока. ( При вычислениях считай, что √3 = 1,7)      (9 пунктов)

8. У фермера есть материал для забора длиной 80 м. Из этого материала надо построить забор вокруг прямоугольного загона, одна сторона которого расположена около каменной стены.

8.1. Площадь загона определяется по формуле S = 80x — 2x2 .

Заполни таблицу

 x  ( м )

5

20

 

  S ( м2 )

350

 

600

 8.2. Нарисуй график функции  S = 80x — 2x2  , если х с [0; 40] . Используй следующий масштаб: 2 клеточки на оси х соответствуют 5 м, а 2 клеточки на оси у соответствуют 100 м2   .

8.3.  Используя график, определи

а) длину загона х, если его площадь равна 750 м2 ;

б) наибольшую возможную площадь загона .  (9 пунктов)

 

ОТВЕТЫ

Часть 1

1. да    2. нет    3. нет     4.  да. 5. нет     6.  — 6         7.  √3

8. 3     9.      x5  = 3/5      10.  a = 3b    11.  20%  12. 80  км/ч  13. x1 = 3; x2 = 4  14.   15. 115  16. 6   17. x с   (2; + ∞)   18. х = 7   19.  1015    20. ab + a — 2b —2    21.   =  90о   22.  /  2 = 136о         23. sin α = 5/6   24. S = 60 (ед. площ.)    25. EF = 20

Часть 2

1.      1.1  12     1.2. 1/5  1.3.  9   1.4. 4   2. 3х + 6  3. ( 1/2  ; 3 )     4. x с   [— 5; — 3]    

 5. CD = 4√3  см;  AB = 2√3  см   6. 15 км/ч   7.    7.1     720 см2      7.2  V = 720√3  см3    

7.3.  нельзя   8.      8.1.        

 8.2.

 

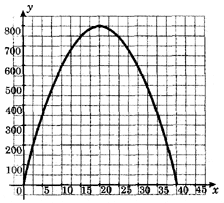
8.3.   а) 15 м или 25 м    б) 800  м2

 
Hosted by uCoz