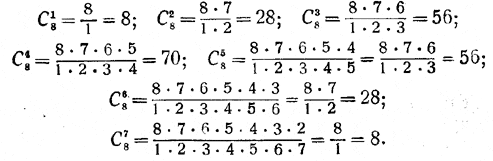ГЛАВА IV.

АРИФМЕТИЧЕСКИЙ ТРЕУГОЛЬНИК ПАСКАЛЯ.

1. Формула сочетаний.

Чтобы не прерывать в дальнейшем (§ 4) изложения, мы сейчас разберём вывод одной весьма важной формулы. Эта формула играет большую роль в различных отделах математики. Начнём с задачи.

Задача. Из семи кандидатов требуется выбрать трёх делегатов на конференцию. Сколько может быть различных результатов выборов (различных случаев)?

Вместо слов «различные случаи» принято говорить «варианты» от латинского слова varius (вариус) —различный.

Решение. Обозначим фамилии кандидатов буквами A,  В, С, D, Е, F, G.  Будем решать задачу постепенно.

Если бы требовалось выбрать только одного делегата, то число вариантов было бы 7, так как может быть выбран любой из семи человек.

Пусть требуется выбрать двух делегатов. Если выбрано лицо А, то к нему можно присоединить или В, или С, или D и т. д. Мы получим, таким образом, варианты АВ, AC, AD, AE, AF, AG (6 вариантов).  

Точно так же, если  уже  выбрано  лицо B,  то к нему можно присоединить любого из остальных, и получаем опять 6 вариантов. То же самое получится, если первым выбрано   лицо С, лицо D и т. д. Если собрать все полученные  таким образом  возможные пары делегатов, то их можно записать в виде прямоугольной таблицы,

В первой строке записаны все пары, в которых первым избранным стоит делегат A; во второй —делегат В и т. д. Всего в таблице 7 строк и 6 столбцов: значит, число возможных пар равно 7•6 = 42. Однако было бы неправильным считать, что и число вариантов (при выборе 2 делегатов из 7 человек) равно 42. В нашей таблице много лишних пар. Если взять, например, пару В и F, то легко увидеть, что она вошла в схему два раза: один раз в порядке (BF), другой раз в порядке (FB). Между тем по смыслу задачи порядок, в котором выбраны делегаты, не должен иметь значения. Так как всякая пара букв входит в таблицу два раза, то искомое число вариантов равно половине найденного числа, т. е. равно

Итак, двух делегатов можно выбрать 21 способом.

Для дальнейшего нужно отметить, какие пары из нашей таблицы мы отбросим и какие оставим. Условимся, например, что из двух пар, содержащих одинаковые буквы, мы будем оставлять ту, в которой буквы расположены в алфавитном порядке;  например, из двух пар BF и FB мы оставим пару BF.

Перейдём теперь к рассмотрению выборов трёх делегатов: Выпишем в один вертикальный столбец все только что полученные 21 пару. К каждой из этих пар делегатов нужно добавить третьего, т. е. приписать одну из остающихся пяти букв. Получим таблицу:

В этой таблице 21 строка и 5 столбцов, содержащих интересующие нас тройки букв: число троек букв равно

Нo и на этот раз мы получили много лишних троек. Если, например, взять тройку букв A, D, G, то в нашей таблице она содержится 3 раза. В самом деле: первые две буквы должны быть обязательно в алфавитном порядке.  Поэтому в таблице найдутся такие тройки:

1) буква A стоит в конце, остальные две буквы стоят в алфавитном порядке: DGA;
2) буква D стоит в конце, остальные две буквы стоят в алфавитном порядке: AGD;
3) буква G стоит в конце, остальные две буквы стоят в алфавитном порядке: ADG.

Так как каждая тройка букв будет встречаться в таблице 3 раза, то число различных по составу троек, т. е. искомое число вариантов, получим, разделив выше найденное число  на 3. Значит, число вариантов равно    Eсли напишем еще в знаменателе множитель 1 (что не изменяет величины дроби), то получим очень удобную для запоминания дробь

Число вариантов выбора 3 элементов из 7 (в нашем случае 3 делегатов из 7 человек) принято в математике обозначать знаком С₇³; буква С есть начальная буква французского слова combinaison — комбинация, сочетание. Говорят: найти число  сочетаний  из  7 элементов по 3.

Пишут:

Точно так же может быть решена задача: найти число сочетаний из 10 элементов по 3.    Получим  

Если требуется найти число сочетаний из 10 элементов по 4, т. е. С₁₀⁴, то надо будет построить таблицу из четвёрок букв. Подобно тому, как в таблице из троек букв, в которой первые две буквы каждой тройки были поставлены в алфавитном порядке, каждое сочетание встречалось ровно три раза, так и в таблице из четвёрок букв, в которой первые три буквы стоят в алфавитном порядке, каждое сочетание встречается ровно четыре раза. В самом деле, на конце четвёрки может стоять первая, вторая, третья или четвёртая буквы. Остальные буквы стоят перед ней в определённом порядке.

Таблица, содержащая четвёрки, будет содержать С₁₀³ • 7 четвёрок, потому что к каждому сочетанию из трёх букв, расположенных в алфавитном порядке, можно приписать любую, не входящую в эту тройку букву; так как всех элементов 10, то элементов, не входящих в данную тройку, 7, и, следовательно, из всех троек получается С₁₀³ • 7 четвёрок.

Но чтобы найти число различных четвёрок, нужно ещё полученное число С₁₀³ • 7 разделить на 4: ведь каждая четвёрка встречается в таблице 4 раза. Таким образом,

Число сочетаний из 20 по 5 может быть получено подобным   же   образом; оно напишется так:    

Эту дробь запишем в другой форме:

В этой дроби в числителе столько же множителей, как и в знаменателе.

Нетрудно составить   формулу   для   числа   сочетаний из п элементов по k (п и k — любые целые числа, k < п):

Следствие. Будем рассматривать, например, числа сочетаний из 8 элементов:

Таким образом, С₈⁵ = С₈³;   С₈⁶ = С₈²;    С₈⁷ = С₈¹.

Эти равенства можно вывести и путём рассуждения: например, С₈⁵ может означать число вариантов выбора из 8 человек 5 делегатов на конференцию. Но если 5 человек уедут на конференцию, то останутся 3 человека. Каждому новому составу выбранных 5 делегатов соответствует новый состав остающихся трёх, и обратно.

Поэтому вместо того, чтобы выбрать 5 делегатов, уезжающих на конференцию, можно выбирать трёх делегатов, остающихся на месте. Получим то же число вариантов:
С₈⁵ = С₈³. Таким же рассуждением можно показать, что
С₈⁶ = С₈²; С₁₀⁷ = С₁₀³; С₂₀¹⁶ = С₂₀⁴  и т. д.

К полученным числам сочетаний из 8 элементов мы добавим ещё два числа:

1.Число С₈⁸, т. е. число сочетаний из 8 элементов по 8; это число, очевидно, равно 1.

2.Число  С₈⁰.   Оно даёт ответ на  вопрос: сколько существует различных способов  не  послать  ни одного делегата на конференцию? Очевидно, только один способ не посылать никого. Добавив числа С₈⁸ и С₈⁰, мы получаем полную строку чисел сочетаний из 8 элементов:

С₈⁰, С₈¹, С₈², С₈³, С₈⁴, С₈⁵, С₈⁶, С₈⁷, С₈⁸.

или

Группы чисел такого рода могут быть составлены не только для числа 8, но и для любого целого числа. Мы встретимся с ними в настоящей главе при разборе замечательной формулы Паскаля.